Часть 2:
Урок 1:
1
2
3
4
5
6
7
8
9
10
10
10
11
12
13
14
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 4:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 5:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 7:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 8:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 10:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 11:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Урок 13:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 14:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 15:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 16:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 17:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 18:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 19:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 20:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 22:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 23:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 24:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 25:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 26:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 27:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 28:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 29:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 30:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 31:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 32:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 33:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 34:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 35:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 36:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Дополнительное ГДЗ
- Часть 1. Страницы учебника
34
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
- Часть 2. Страницы учебника
34
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
- Часть 3. Страницы учебника
34
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40-41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
- 40-41
Начальная школа уже с первых лет связана с постоянно увеличивающейся нагрузкой. Причем уже в младших классах приходится решать много нелегких заданий по разным дисциплинам, в том числе и по математике. Это один из самых сложных предметов в программе и неудивительно, что его изучение не всем дается легко. Четвероклассникам из-за ожидающихся вскоре контрольных работ и экзаменов нередко приходится нанимать репетиторов, задействовать решебники. Индивидуальные занятия требуют финансовых трат, а вот онлайн-сборник с ГДЗ по математике (4 класс) — нет.
Викторина «Хочу все знать». а) На земном шаре обитают птицы, которых в народе называют составителями прогноза на лето. Они строят гнезда из песка. Замечено, что обычно высота гнезда зависит от того, каким будет лето − сухим или дождливым. Если лето ожидается дождливым, то гнезда строятся высокими, чтобы их не могла затопить вода, а если лето ожидается засушливым, то гнезда строятся более низкими. Расшифруй название этих птиц, выполнив деление и сопоставив полученным ответам буквы на диаграмме:
б) Самое крупное на суше животное − африканский слон. Узнай высоту и длину тела африканского слова (в сантиметрах) и его массу (в килограммах). в) Масса новорожденного слоненка в 60 раз меньше массы взрослого слона. Найди массу новорожденного слоненка и определи, на сколько меньше массы взрослого слона. г) Вырази высоту и длину тела взрослого слона в метрах и сантиметрах, а массу его тела − в тоннах.
Уроки по математике в четвертом классе общеобразовательной школы – это, прежде всего, арифметические операции в уме и в столбик с многозначными целыми (натуральными) числами. Ученики должны научиться идеально и безошибочно складывать, вычитать, умножать и находить целочисленный остаток от деления. Эти практические навыки неоднократно понадобятся в средних и даже старших классах общеобразовательной школы. Они тренируют ум и позволяют развить способности к точному и строгому мышлению.
Именно в начальной школе крайней важно достичь хорошей успеваемости по математике, чтобы образовательные «хвосты» не тянулись за ребенком всю оставшуюся жизнь. Непременно поможет в этом решебник, подготовленный по формату ГДЗ (готовых домашних заданий)
Одним из вариантов на ваш выбор является методическое пособие Л. Петерсна, которое подготовила известный в Российской Федерации учебник «Математика, 4 класс».
Что входит в решебник по математике?
Мамы и папы, как правило, предпочитают обращаться к услугам репетиторов, если у их ребенка возникают проблемы с учебой. Но такой подход только еще больше выматывает детей, ведь фактически после того, как закончились одни уроки, они должны идти на другие. При этом есть еще и дополнительные секции и кружки, которые посещает большинство ребят. Таким образом, ученики практически не отдыхают, ведь заканчивают выполнять домашние задания уже после девяти вечера. Некоторые и вовсе сидят до полуночи. Неудивительно, что с утра они чувствуют себя разбитыми и рассеянными. С «ГДЗ по математике 4 класс Учебник Петерсон (Просвещение)» можно решить все эти проблемы.
В решебнике школьники найдут все необходимое для успешного освоения текущей программы:
- верные ответы на все номера учебника;
- подробно расписанные решения;
- наглядные примеры;
- дополнительные комментарии в особо сложных случаях;
- графические и схематические подсказки.
Большим плюсом при работе с пособием считается то, что четвероклассники самостоятельно разбирают все трудные моменты. Как бы не был хорош репетитор, но все равно он будет подсказывать. Решебник же помогает визуализировать всю информацию. Выполнение аналогичных упражнений способствует лучшему пониманию алгоритма. Стоит также отметить, что учащимся не придется никуда ездить, что существенно экономит время и силы. Достаточно просто иметь под рукой любой гаджет с выходом в интернет.
Часть 2
- Урок 1. Деление и дроби
- Урок 2. Нахождение части, которую одно число составляет от другого
- Урок 3. Сложение дробей
- Урок 4. Вычитание дробей
- Урок 5. Правильные и неправильные дроби
- Урок 6. Правильные и неправильные части величин
- Урок 7. Задачи на части
- Урок 8. Смешанные числа
- Урок 9. Выделение целой части из неправильной дроби
- Урок 10. Запись смешанного числа в виде неправильной дроби
- Урок 11. Сложение и вычитание смешанных чисел
- Урок 12. Сложение и вычитание смешанных чисел
- Урок 13. Сложение и вычитание смешанных чисел
- Урок 14. Сложение и вычитание смешанных чисел
- Урок 15. Сложение и вычитание смешанных чисел
- Урок 16. Сложение и вычитание смешанных чисел
- Урок 17. Шкалы
- Урок 18. Числовой луч
- Урок 19. Координаты на луче
- Урок 20. Расстояние между точками числового луча
- Урок 21. Движение по числовому лучу
- Урок 22. Движение по числовому лучу
- Урок 23. Одновременное движение по числовому лучу
- Урок 24. Скорость сближения и скорость удаления
- Урок 25. Скорость сближения и скорость удаления
- Урок 26. Встречное движение
- Урок 27. Движение в противоположных направлениях
- Урок 28. Движение вдогонку
- Урок 29. Движение с отставанием
- Урок 30. Формула одновременного движения
- Урок 31. Формула одновременного движения
- Урок 32. Формула одновременного движения
- Урок 33. Формула одновременного движения
- Урок 34. Формула одновременного движения
- Урок 35. Действия над составными именованными величинами
- Урок 36. Новые единицы площади
Часть 1
- Урок 1. Решение неравенства
- Урок 2. Множество решений
- Урок 3. Знаки > и <
- Урок 4. Двойное неравенство
- Урок 5. Двойное неравенство
- Урок 6. Оценка суммы
- Урок 7. Оценка разности
- Урок 8. Оценка произведения
- Урок 9. Оценка частного
- Урок 10. Прикидка результатов арифметических действий
- Урок 11. Деление с однозначным частным
- Урок 12. Деление с однозначным частным
- Урок 13. Деление на двузначное и трехзначное число
- Урок 14. Деление на двузначное и трехзначное число
- Урок 15. Деление на двузначное и трехзначное число
- Урок 16. Деление на двузначное и трехзначное число
- Урок 17. Оценка площади
- Урок 18. Приближенное вычисление площадей
- Урок 19. Измерения и дроби
- Урок 20. Из истории дробей
- Урок 21. Доли
- Урок 22. Сравнение долей
- Урок 23. Нахождение доли числа
- Урок 24. Проценты
- Урок 25. Нахождение числа по доле
- Урок 26. Нахождение числа по доле
- Урок 27. Дроби
- Урок 28. Сравнение дробей
- Урок 29. Нахождение части числа
- Урок 30. Нахождение числа по его части
- Урок 31. Нахождение числа по его части
- Урок 32. Площадь прямоугольного треугольника
Часть 1:
Урок 1:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 4:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 5:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 7:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 8:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 10:
1
2
3
4
5
6
7
8
9
11
12
13
14
15
Урок 11:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 13:
1
2
3
4
5
6
7
8
9
10
Урок 14:
1
2
3
4
5
6
7
8
9
Урок 15:
1
2
3
4
5
6
7
8
9
Урок 16:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 17:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 18:
1
3
4
5
6
7
8
9
10
11
Урок 19:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 20:
1
2
3
4
5
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 22:
1
2
3
4
5
6
7
8
9
10
12
13
14
15
16
Урок 23:
1
2
3
4
5
6
7
8
9
Урок 24:
1
2
3
4
5
6
7
8
9
10
11
Урок 25:
1
2
3
4
5
6
7
8
9
10
Урок 26:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 27:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 28:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 29:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 30:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 31:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 32:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Часть 3
- Урок 1. Сравнение углов
- Урок 2. Развернутый угол. Смежные углы
- Урок 3. Измерение углов
- Урок 4. Угловой градус
- Урок 5. Транспортир
- Урок 6. Транспортир
- Урок 7. Транспортир
- Урок 8. Транспортир
- Урок 9. Транспортир
- Урок 10. Круговые диаграммы
- Урок 11. Столбчатые и линейные диаграммы
- Урок 12. Игра «Морской бой». Пара элементов
- Урок 13. Передача изображений
- Урок 14. Координаты на плоскости
- Урок 15. Построение точек по их координатам
- Урок 16. Точки на осях координат
- Урок 17. Точки на осях координат
- Урок 18. График движения
- Урок 19. График движения
- Урок 20. График движения
- Урок 21. График движения
- Задачи на повторение
Какими достоинствами обладает онлайн гдз по математике для 4 класса автора Петерсон?
Хотя многие специалисты и родители школьников по-прежнему неоднозначно оценивают эффективность решебника, указывая на то, что ученики хотят переписать готовый ответ, а не размышлять над этим самостоятельно, среди тех, кто ценит полезность, появляется все больше и больше сторонников этого ресурса. Их аргументы:
- возможность пользоваться ресурсом круглосуточно, в любой день недели;
- экономия семейного бюджета, так как этот материал является действенной альтернативой или серьезным дополнением к образовательной помощи, платным кружкам;
- значимость информации, ее соответствие требованиям положений об образовательных стандартах, в том числе – и оформление решений;
- быстрый поиск ответа на самое сложное задание, ознакомление с алгоритмом решения и использование полученной информации в дальнейшей учебе, для решения аналогичных задач;
- грамотный поиск, чтобы быстро найти и использовать желаемый результат.
Обратившись один раз за помощью к решебникам, нельзя не убедиться в том, насколько полезной для обучения является собранная в них информация. С готовыми ответами еуроки ГДЗ любой ребенок сможет справиться с итоговыми контрольными по самым сложным темам и показать хороший результат.
Часть 2:
Урок 1:
1
2
3
4
5
6
7
8
9
10
10
10
11
12
13
14
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 4:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 5:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 7:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 8:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 10:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 11:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Урок 13:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 14:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 15:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 16:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 17:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 18:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 19:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 20:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 21:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 22:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 23:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 24:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 25:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 26:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 27:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 28:
1
2
3
4
5
6
7
8
9
10
11
12
13
Урок 29:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 30:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 31:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 32:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 33:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 34:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 35:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 36:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ГДЗ по математике за 4 класс учебник Петерсон Л. Г. (Ювента) для практикантов
Если ребята желают достичь наилучших результатов в учебе, но они не знают, с чего начать, то отличным решением всех проблем станет виртуальный наставник под редакцией Петерсон. Этот онлайн-справочник был разработан одним из высококвалифицированных специалистов. Он прекрасно понимал, что пособие с ответами пригодится для более слабых учащихся начальной школы, поэтому старался изложить информацию максимально простым и понятным языком. По этой причине порталом могут пользоваться не только малыши, но и учителя. Так как решебник полностью соответствует всем строгим правилам и требованиям ФГОС, то его могут использовать как высококвалифицированные педагоги, так и новички. Благодаря этому справочнику им удастся:
- составить свою методику обучения в школе;
- сделать свои занятия более интересными;
- подобрать вопросы для тестов и практических;
- провести устный или письменный опрос в классе;
- проверить тетради школьников с выполненными заданиями.
Ребятам обязательно это нужно взять на заметку. Благодаря такому чудо-справочнику они смогут подготовиться к любой проверке в классе. Чтобы материалы всегда находились под рукой, ребятам нужно вооружиться любым современным устройством, будь то смартфон, планшет или нетбук. Найти верный ответ на любой вопрос проще простого. Для этого школьнику необходимо нажать на номер того или иного упражнения. Практически мгновенно на экране устройства появятся не только ответы, но и комментарии к решенным упражнениям. Все, что написано в книжечке, поможет преодолеть возникающие трудности на пути к получению знаний!
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
\(n(U)\;=\;100\\n(Р)\;=\;28,\;n(Ф)\;=\;42,\;n(К)\;=\;30\\n\;(Р\;\cap\;Ф)\;=\;10,\;n(Р\;\cap\;К)\;=\;8,\;n\;(Ф\;\cap\;К)\;=\;5\\n\;(Р\;\cap\;Ф\;\cap\;К)\;=\;3\)
Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна
Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено
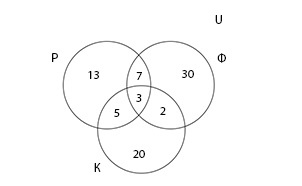
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
\(n(Р\;\cup\;Ф\;\cup\;К)\;=\;13\;+\;7\;+\;30\;+5\;+\;3\;+\;2\:+\;20\;=\;80\)
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
\(n(U\;\backslash\;(Р\;\cup\;Ф\;\cup\;К))\;=\;100\;-\;80\;=\;20\)
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
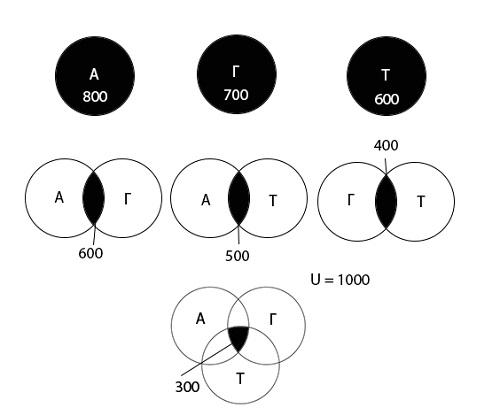
Теперь используя диаграмму, обозначим область, которую необходимо найти:
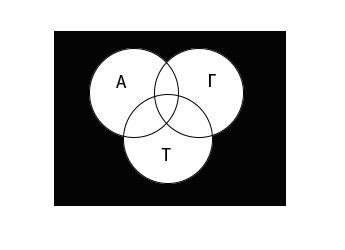
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
- Область А = 0, Г = 0, Т = 1: школьников нет.
- Область А = 0, Г = 1, Т = 0: школьников нет.
- Область А = 0, Г = 1, Т = 1: 100 школьников.
- Область А = 1, Г = 0, Т = 0: школьников нет.
- Область А = 1, Г = 0, Т = 1: 200 школьников.
- Область А = 1, Г = 1, Т = 0: 300 школьников.
- Область А = 1, Г = 1, Т = 1: 300 школьников.
Теперь внесем значения всех областей в диаграмму:
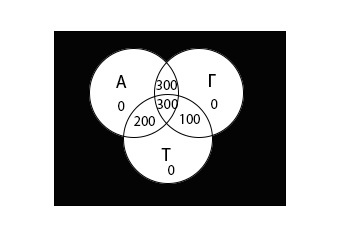
Определим x:
\(x\;=\;U\;-\;(A\;\cup\;Г\;\cup\;Т)\;\)
При U — универсум
U = 1000
\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)
x = 1000 — 900 = 100
Приоритетные группы пользователей онлайн справочника
В числе тех, кто может постоянно использовать готовые ответы к рабочей тетради по математике для 4 класса автора Петерсон, такие группы пользователей:
четвероклассники, которые не совсем понимают, как правильно решать примеры или задачи, либо по каким-то причинам пропустили пояснение темы на уроке учителем и теперь не могут самостоятельно разобраться с предлагаемым материалом;
родители четвероклассников, желающие лично контролировать, несколько их ребенок вникает в суть темы, разбирается в правилах и умеет применять математические формулы на практике;
школьники старших классов, которым важно вернуться к повторению ранее изученного материала, например, перед написанием самостоятельной или контрольной работы;
участники олимпиад, математических конкурсов для подготовки к решающим испытаниям. Такой сборник поможет выявить возможные пробелы в знаниях и вовремя вернуться к более подробному рассмотрению тематического материала;
учителя начальной школы, репетиторы, которым необходимо качественно проверить существенный объем готовых ученических работ за короткий промежуток времени.
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств \(A\;\wedge\;B\)
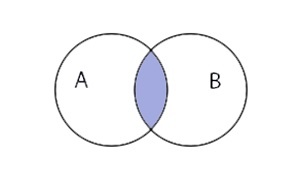
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B
Графически отметим дизъюнкцию, заштриховав оба круга цветом.
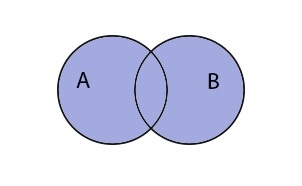
Теперь отобразим инверсию, заштриховав область за пределами множеств.
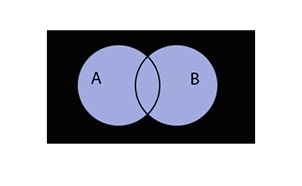
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом
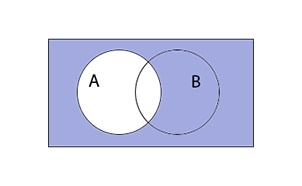
Проведем аналогичную операцию с множеством B.
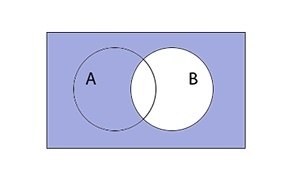
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
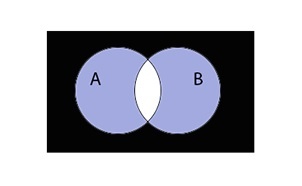
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Готовые домашние задания по пособию Петерсона
Учебник удобно структурирован на 3 части, где есть теория и практические упражнения для закрепления материала. В первую очередь решебник пригодится четверокласснику. Он сможет улучшить средние баллы, научиться быстрее решать однотипные задания, эффективнее готовиться к занятиям, рациональнее расходовать свое время. Также учителям-математикам, преподающим предмет для 4 класса по пособию Петерсона, готовые ответы будут полезными в целях экономии времени на проверку домашки и подготовки материала ученикам. Все материалы в нем составлены в соответствии с Федеральным государственным образовательным стандартом. По структуре он повторяет учебник: ресурс разделен на три части, в каждой из которых имеются разобранные задания. Также тут есть ответы на проверочные и контрольные работы после всех параграфов.
Часть 3:
Урок 1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Урок 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 4:
1
2
4
5
6
7
8
9
10
11
12
13
14
Урок 5:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Урок 6:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 7:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 8:
1
2
3
4
5
6
7
8
10
11
12
13
14
15
16
Урок 9:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Урок 10:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 11:
1
2
3
4
5
6
7
Урок 12:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Урок 13:
1
2
3
4
6
7
8
9
10
11
12
Урок 14:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 15:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Урок 16:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Урок 17:
1
2
3
4
5
7
9
10
11
12
13
Урок 18:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 19:
1
2
3
4
5
6
7
8
9
10
11
12
Урок 20:
1
2
3
4
5
6
7
8
9
Урок 21:
1
2
3
4
5
6
7
8
9
Повторение:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
Что такое диаграммы Эйлера-Венна
Определение
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
- В первую очередь необходимо начертить диаграмму, заштриховав все множества, находящиеся в левой части равенства.
- Следующим шагом будет начертание другой диаграммы и штриховка всех множеств, которые находятся в правой части равенства.
- В случае, когда на диаграммах заштрихована одна и та же область, торжество истинно.
Дополнение множества
Дополнением к множеству A является множество \(\overline A\), которое состоит из элементов, не входящих в А.
\(\overline A\;=\;\left\{x\;\vert\;x\;\not\in\;A\right\}\)
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
\(\overline A\;=\;U\;\backslash\;A\)
Таким образом выглядит дополнение \(\overline A\) графически:
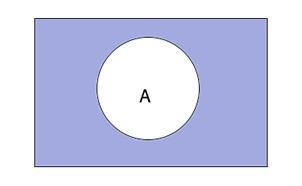
Для кого предназначен решебник по математике?
Среди тех, кто использует быстрые ответы к учебнику по математике 4 класс Петерсон, следующие категории пользователей:
- родители четвероклассников стремятся проверить правильность поставленных учителем задач, не углубляясь слишком сильно в программу курса, при этом хочется быть уверенным в результате;
- преподаватели, которым необходимо быстро проверить большое количество представленных рабочих тетрадей, не рискуя качеством своей работы;
- дети, занимающиеся в профильных кружках по математике, для которых данный предмет является основной специальностью, что позволяет глубже и полнее понимать интересующие их темы и разделы, которые были изучены;
- четвероклассники, интересующиеся этой наукой, желающие в будущем глубоко овладеть ею, а возможно, даже сделать ее основой своей будущей профессии;
- школьники, которые занимаются математикой в рамках школьной программы, и им непросто усваивать науку, но готовы разбираться во всех тонкостях и нюансах, осваивать новые знания.
Изучать дисциплину сложно. Для того, чтобы понимать предметный материал и иметь положительные результаты, к обучению необходимо подойти со всей серьёзностью. Нельзя упускать не малейшей детали, иначе в будущем будут проблемы. А хорошим подспорьем в учёбе станут ГДЗ по математике 4 класс самостоятельные и контрольные работы Петерсон 1, 2 часть. Решебник имеет в своём содержании подробные и досконально расписанные онлайн-ответы, которые юный школьник найдёт без труда по номеру упражнения. Они помогут:
- проверить правильное выполнение домашней работы;
- разобрать и понять сложную тему;
- тщательным образом подготовиться к предстоящему уроку;
- закрепить пройденный материал.
Математика – это основной предмет школьной программы. Она изучает количественные отношения, различные величины и пространственные формы. С самого первого класса ребята учатся складывать и вычитать, решать задачки, сравнивать. Математика является фундаментальной для многих смежных дисциплин, это и обуславливает столь раннее её изучение.
Контроль знаний – это неотъемлемая часть учебного процесса. Чаще всего его проводят с помощью специальных пособий. К числу подобных относятся различные проверочные. Разноплановые работы представлены по всему учебному курсу и помогут выявить пробелы и недочёты в понимании дисциплины и, если таковые имеются, провести коррекцию ошибок.
Математика 4 класс
Решебник – это не книга, которую стоит опасаться как огня и моментально отбирать у ребенка, как только вы заметили его использования. А даже наоборот – полезное пособие, способное улучшить успеваемость, и повысить уровень знаний. Удивляетесь, как такое возможно? Все очень просто. ГДЗ по математике для 4 класса от Петерсон Л. позволит школьнику сделать следующее:
- выучить материал, который он пропустил: для начала откройте учебник и тщательно изучите представленный там теоретический материал, после чего постарайтесь самостоятельно решить несколько заданий. И только после выполнения этих двух пунктов откройте сборник, сверьте выполненные упражнения с готовыми ответами и разберитесь с допущенными ошибками;
- далеко не все учителя умеют доступно объяснять тему, и порой школьник приходит домой совершенно без знаний. Работая по тому же принципу, что описан выше, ребенок сможет изучить пройденный раздел и закрепить материал в памяти надолго;
- проверка домашнего задания, чтобы исключить наличие случайных ошибок и опечаток, способных значительно снизить оценку;
- теперь четвероклассник сможет стать самостоятельным, ведь при возникновении проблем с домашкой, больше не придется бежать за помощью к родителям, все функции проверки выполняет решебник.
Также колоссальную пользу пособие приносит учителям, которые из-за своей работы уже совсем забыли про личную жизнь и полноценный отдых и только знают, что целыми днями проверять тетради с контрольными и домашними работами. С помощью ГДЗ этот процесс значительно сократится по времени, да и сил теперь затрачивать придется намного меньше, а значит, что учитель наконец-то станет счастливый, что положительно скажется на его профессиональных навыках.
Решебник для 4 класса Л. Петерсона составлен по нормам ФГОС и полностью соответствует учебнику от этого же автора. Найти пособие не сложно, ведь оно размещено в онлайн-доступе, и для его использования теперь достаточно просто зайти в интернет. Учеба еще никогда не была такой простой и при этом эффективной.





















