Страница 34
Найди среди прямоугольников такие, у которых все стороны равны. Выпиши их номера.
1, 4
Задание 3.
- 1) Начерти в тетради квадрат, длина стороны которого 4 см.
- 2) Найди периметр этого квадрата.
2) 4 + 4 + 4 + 4 = 16 (периметр квадрата)
Задание 4.
Вычисли и проверь сложение вычитанием, а вычитание сложением.
| 38 + 24 = 62 | 75 — 26 = 49 | 14 + 26 = 40 | 82 — 79 = 3 |
| 62 — 38 = 24 | 49 + 26 = 75 | 40 — 14 = 26 | 79 + 3 = 82 |
Задание 5.
Вспомни правила о порядке выполнения действий и вычисли значения выражений.
| 100 — (60 + 24) = 16 | 60 — (80 — 37) = 17 | 9 + 7-8 |
| (70 + 25) — 90 = 5 | 70 — (50 — 6) = 26 | 9 — 4 + 7 = 12 |
Задание 6.
Составь задачу по выражению и реши её.
| 1) 100 — (25 + 15) | 2) (20 + 20) + 50 |
|
|
Реши уравнения.
| 75 — х = 75 | 4 + х = 64 | 89 — y = 0 |
| x = 75 — 75 | x = 64 — 4 | y = 89 + 0 |
| x = 0 | x = 60 | y = 89 |
Страница 41
Задание 9.
В детский сад привезли два бидона с молоком, по 20 л в каждом. За завтраком дети выпили 12 л молока. Сколько литров молока осталось? Реши задачу разными способами.
-
- Способ 1.
- 1) 20 + 20 = 40
- 2) 40 — 12 = 28
- Выражение: (20 + 20) — 12 = 28
- Ответ: 28 бидонов осталось.
-
- Способ 2.
- 1) 20 — 12 = 8
- 2) 20 + 8 = 28
- Выражение: (20 — 12) + 20 = 28
- Ответ: 28 бидонов осталось.
Задание 10.
В одной группе детского сада было 20 детей, а в другой — на 3 ребёнка меньше. Сколько всего детей было в двух группах?
- 1) 20 — 3 = 17
- 2) 20 + 17 = 37
- Выражение: 20 + (20 — 3) 37
- Ответ: в двух группах было 37 детей.
Задание 11.
Книга стоит □ р., пенал — на 10 р. дороже книги, а альбом на 5 р. дешевле пенала. Сколько стоит альбом? Дополни задачу и реши её.
Книга стоит 31 р., пенал — на 10 р. дороже книги, а альбом на 5 р. дешевле пенала. Сколько стоит альбом?
- Решение:
- 1) 31 + 10 = 41
- 2) 41 — 15 = 26
- Выражение: 31 + 10 — 15 = 26
- Ответ: альбом стоит 26 рублей.
Задание 12.
Утром в отделе игрушек было 12 легковых машинок и 20 грузовых. За день было продано 8 легковых и 12 грузовых машинок. Сколько легковых и сколько грузовых машинок осталось?
- 1) 12 — 8 = 4
- 2) 20 — 12 = 8
- Ответ: осталось 4 легковых машинки и 12 грузовых машинок.
Задание 13.
В киоске было 90 гвоздик. До обеда продали 40 гвоздик, а после обеда ещё 28 гвоздик. Сколько гвоздик осталось в киоске?
- 1) 40 + 28 = 68
- 2) 90 — 68 = 22
- Выражение: 90 — (40 + 28) = 22
- Ответ: 22
Задание 14.
Используя таблицу, составь выражения и вычисли их значения.
| 48 + 26 = 74 | 48 + 28 = 76 | 48 + 30 = 78 |
| 46 + 34 = 80 | 44 + 34 = 78 | 42 + 34 = 76 |
Квадратный сантиметр, дециметр, метр
Какой меркой лучше измерить площадь фигуры квадрата и прямоугольника?
В 18 веке на Руси вводилась основная мера измерения площади — десятина и четь. Но поля крестьян были неровными, поэтому часто мерками служила урожайная копна. Народ изобретал особые мерки: выть, соха, обжа, коробь, веревка, жеребья. Сейчас мы не используем этих мер.

Начертите прямоугольник со сторонами 5см и 4см. Какими мерками можно измерить фигуру?
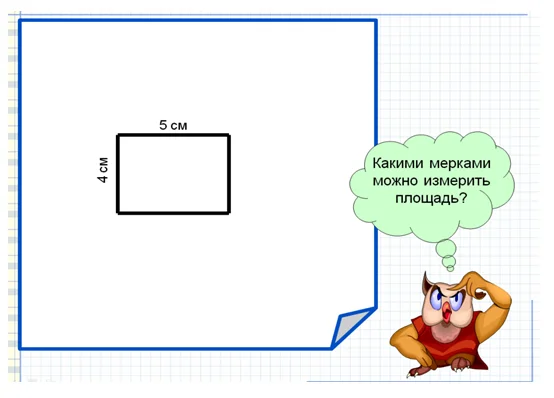
Посмотрите на рисунок, утенок измерил прямоугольник с помощью треугольников, ежонок — квадратами, а котенок — прямоугольниками.
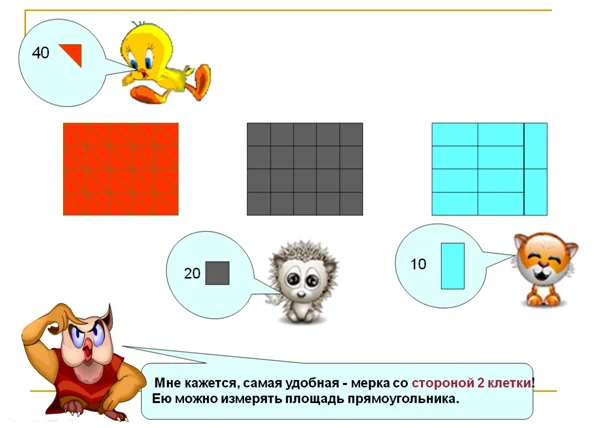
Посчитаем, сколько единичных мерок находится в прямоугольнике. У животных получились разные величины: 40, 20, 10.
Всегда ли удобно определять площадь фигуры произвольными мерками?
Конечно, нет.
Вывод: значение величины зависит от выбранной мерки. Чтобы сравнить, нужно договориться об одинаковом способе измерения.
Всегда ли для определения площади фигуры подходит клетка?
Да.
Какого размера должна быть клетка?
Я предлагаю измерять как ежик, квадратами по 2 клеточки.
Измерьте длину и ширину этого квадратика. Что получилось?

Длина и ширина равна 1 см.
Единицей измерения площади еще 4-5 тысяч лет тому назад жители древнего города Вавилона считали квадрат, так как именно квадрат имеет превосходные признаки: четыре стороны равны межу собой, четыре прямых угла; можно провести ось и найти центр симметрии. Форма квадрата без изъянов, совершенна, поэтому его легко начертить и плотно покрыть фигуры любой формы.
Если у квадратика сторона 1см – площадь его равна квадратному сантиметру.
1 квадратный сантиметр сравним с ноготком взрослого человека.
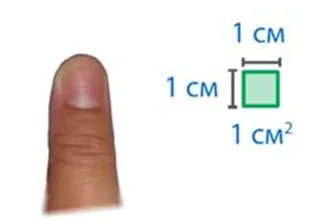
Записывается площадь 1 квадратного сантиметра так:
S = 1 кв. см или S = 1 см2
Латинская буква «эс» обозначает площадь, двойка в правом верхнем углу — две величины: длину и ширину.
Начертите квадрат со стороной 10 сантиметров.

Квадратный дециметр (1 дм 2) — это квадрат со стороной 1 дм или 10 см.
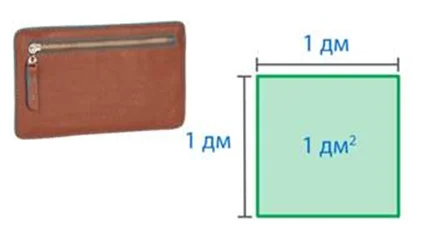
Квадратный метр (1 м 2) — это квадрат со стороной 1 м или 10 дм. В квадратных метрах обозначается площадь в жилых помещениях, например: в комнатах, коридорах. Эта мерка подойдет для измерения дачного участка, спортивного зала, территории сквера.
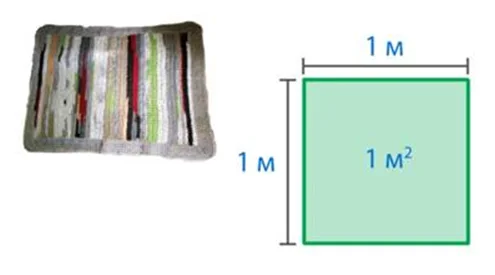
А при строительстве школ важно учитывать, сколько квадратных метров должно быть в классе, если для одного ученика по санитарным правилам нужно 4 квадратных метра. Вы хорошо справляетесь с заданиями
Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку
Вы хорошо справляетесь с заданиями. Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку.
Физкультминутка
Поднимитесь, вверх потянитесь,
Вперед наклонитесь.
Ниже, ниже тянитесь,
Достаньте мизинцем до пятки.
Получилось? Тогда все в порядке.
Выпрямитесь, грудью вздохните,
Руки шире в стороны разведите.
Соедините в замок на лопатках.
Получилось? Тогда все в порядке.
Глазки зажмурьте, спокойно постойте.
Отдохнули? Теперь посчитайте площадки.
МАТЕМАТИКА
Единицы площади / стр. 41
Единицы площади — это квадраты, стороны которых измеряются единицами длины.
Назови по порядку известные тебе единицы площади, начиная с квадратного сантиметра.
Для измерения больших площадей используют квадратный километр.
Это квадрат, сторона которого равна 1 км.
Слова «квадратный километр» сокращённо при числе записывают так: 1 км2, 8 км2, 140 км2.
В квадратных километрах измеряют, например, площади государств: так, Россия занимает площадь более 17 000 000 км2, а Франция — 551 000 км2.
Для измерения маленьких площадей используют квадратный миллиметр — это квадрат, сторона которого 1 мм. Слова «квадратный миллиметр» при числах сокращённо записывают так: 1 мм2, 9 мм2, 70 мм2.
Вычисли, сколько в 1 см2 квадратных миллиметров, зная, что 1 см = 10 мм.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
184.
Вычисли, сколько в 1 км2 квадратных метров, зная, что 1 км = 1 000 м.
185.
На рисунке 1 покажи 1 мм2, 1 см2, половину квадратного сантиметра, четвёртую часть квадратного сантиметра и запиши, сколько это квадратных миллиметров.

186.
Рассмотри рисунок 2. Площадь какой фигуры больше и на сколько квадратных миллиметров?
187.
Найди площадь прямоугольника ABCD и квадрата КМОЕ в квадратных миллиметрах и вырази её в квадратных сантиметрах.
188.
Вырази:
1) в квадратных метрах: 5 км2, 48 км2, 4 км2, 120 м2;
2) в квадратных миллиметрах: 8 см2, 15 см2, 23 см2, 20 мм2.
189.
Сделай схематический чертёж по задаче и реши её.
1) Расстояние между двумя городами 420 км. Поезду на пути из одного пункта в другой осталось пройти 180 км. На сколько километров больше поезд прошёл, чем ему осталось пройти?
2) Когда от мотка тесьмы отрезали 3 раза по 2 м, в нём осталось с м. Запиши выражением, сколько метров тесьмы было в мотке сначала.
190.
![]()
191.
Выполни деление с остатком и проверь решение:
80 : 9 70 : 60 952 : 8 879 : 6 809 : 7 968 : 9
192.
Найди число, которое:
1) больше, чем 567, на 94;
2) меньше, чем 356, в 4 раза.
193.
Найди на чертеже прямые, острые и тупые углы. Запиши название каждого угла.
Головоломка:
1.
Используя знаки действий и скобки, запиши:
1) число 24 четырьмя тройками или тремя двойками (например, 24 = 33 — 3 • 3);
2) числа 20, 10, 810, 1 008 четырьмя девятками.
3) число 1 000 пятью девятками или шестью пятёрками.
2.
1) Как переложить 2 палочки, чтобы получилось 5 одинаковых квадратов?
2) В полученной фигуре убери 2 палочки так, чтобы осталось 3 квадрата.
Страница 42
Задание 15.
Сравни выражения в каждом столбике. Найди значение первого из них и вычисли значения остальных самым лёгким способом.
| 8 + 57 = 65 | 97 — 27 = 70 | 89 — 13 = 76 |
| 18 + 57 = 75 | 97 — 30 = 67 | 79 — 13 = 66 |
| 28 + 57 = 85 | 97 — 33 = 64 | 69 — 13 = 56 |
| 38 + 57 = 95 | 97 — 36 = 61 | 59 — 13 = 46 |
Задание 16.
Запиши выражения и вычисли их значения.
- 1) Из числа 86 вычесть сумму чисел 42 и 4.
- 2) К разности чисел 54 и 20 прибавить 60.
- 1) 86 — (42 + 4) = 40
- 2) (54 — 20) + 60 = 94
Какие однозначные числа можно записать в окошки, чтобы равенства были верными?![]()
| 43 + 11 — 4 = 50 | 39 — 8 + 14 = 45 |
Задание 18.
В автобусном парке было 78 автобусов. Сначала на маршруты вышло 30 автобусов, а потом ещё 40. Сколько автобусов осталось в парке?
- 1) 78 — 30 = 48
- 2) 48 — 40 = 8
- Выражение: 78 — 30 — 40 = 8
- Ответ: в парке осталось 8 автобусов.
Задание 19.
- 1) Составь выражение и найди его значение: к разности наибольшего двузначного числа и числа 77 прибавить наименьшее двузначное число.
- 2) Найди значения выражений 15 + a — 13 и b — 2 + 18 при a = 5, a = 10, a = 30 и b = 32, b = 43, b = 52.
1) 99 — 77 + 10 = 32
| 15 + 5 — 13 = 7 | 32 — 2 + 18 = 48 |
| 15 + 10 — 13 = 12 | 43 — 2 + 18 = 59 |
| 15 + 30 — 13 = 32 | 52 — 2 + 18 = 68 |
Страница 44
Задание 28.
В школьном уголке природы три аквариума: в первом 8 рыбок, во втором на 3 рыбки меньше, чем в первом, а в третьем столько рыбок, сколько в первом и втором аквариумах вместе. Сколько рыбок в третьем аквариуме?
- 1) 8 — 3 = 5 (рыбок во втором аквариуме)
- 2) 8 + 5 = 13
- Выражение: (8 — 3) + 8 = 13
- Ответ: 13 рыбок в третьем аквариуме.
Задание 29.
Составь задачу по краткой записи и реши её.
| 1) У Оли — 20 к. | 2) У Миши — 5 р. |
| У Ани — на 5 к. меньше | У Коли — 50 р. |
| Всего — ? | Истратили — 20 р. |
| Осталось — ? |
1) У Оли было 20 копеек, а у Ани на 5 копеек меньше. Сколько денег у Оли и у Ани вместе.
|
2) Коля с Мишей истратили 20 рублей. Сколько денег у них осталось, если у Коли было 50 рублей, а у Миши 5.
|
Задание 30.
Составь задачу по выражению и реши её.
| 1) 100 — (15 + 30) | 2) 50 + (30 + 20) |
- 1)
У Саши было 100 рублей. Сначала он потратил 30 рублей потом еще 15. Сколько денег осталось у Саши?- Решение:
- 1) 30 + 15 = 45
- 2) 100 — 45 = 55
- Ответ: у Саши осталось 55 рублей.
- 2)
В магазине до обеда продали 20 кг яблок, а после обеде еще 30. Сколько кг яблок было в магазине сначала, если в конце дня осталось 50 кг?- Решение:
- 1) 20 + 30 = 50 (продали яблок за день)
- 2) 50 + 50 = 100
- Ответ: 100 кг яблок было в магазине с утра.
Задание 31.
- 1) Составь задачу по чертежу и реши её.
- 2) Составь две задачи, обратные данной, реши их.
- 1) Велосипедист и пешеход вышли на встречу друг другу. Когда они встретились, велосипедист проехал 70 м, а пешеход прошел 28 м. Какое расстояние они преодолели вместе.
- Решение:
- 1) 70 + 28 = 98
- Ответ: сначала между ними было расстояние 98 метров.
- 2) Велосипедист и пешеход вышли на встречу друг другу. Когда они встретились, велосипедист проехал 70 м. Какое расстояние преодолел пешеход, если сначала между ними было 98 метров.
- Решение:
- 1) 98 — 70 = 28
- Ответ: пешеход преодолел 28 метров.
- 3) Велосипедист и пешеход вышли на встречу друг другу. Когда они встретились, пешеход прошел 28 м. Какое расстояние преодолел велосипедист, если сначала между ними было 98 метров.
- Решение:
- 1) 98 — 28 — 70
- Ответ: велосипедист преодолел 70 метров.
Ответы к стр. 90
426. Вычисли и выполни проверку.960120 : 8 70209 : 9 56630 : 7 453520 : 5
— 960120|8 8 |120015 —16 16 _12 8 _40 40 0
Проверка: ×120015 8 960120
— 70209|9 63 |7801 —72 72 _9 9 0
Проверка: ×7801 9 70209
— 56630|7 56 |8090 —63 63 0
Проверка: ×8090 7 56630
— 453520|5 45 |90704 —35 35 _20 20 0
Проверка: ×90704 5 453520
427. Узнай число, которое:1) на 85 больше, чем 19600;2) в 8 раз меньше, чем 1600;3) на 5000 меньше, чем 12000;4) в 9 раз больше, чем 9000.
1) 19600 + 85 = 19685;
2) 1600 8 = 200;
3) 12000 − 5000 = 7000;
4) 9000 • 9 = 81000.
428. Ане 12 лет. Она в 3 раза старше брата. На сколько лет Аня старше брата?
1) 12 3 = 4 (г.) − возраст брата
2) 12 − 4 = 8 (л.) − Аня старше брата
О т в е т: Аня старше брата на 8 лет.
429. Спектакль для детей начался в 11 ч и закончился в 12 ч 35 мин. Сколько времени длился этот спектакль?
12 ч 35 мин − 11 ч = 1 ч 35 мин − продолжительность спектакля
О т в е т: спектакль длился 1 ч 35 мин.
430. Рабочие должны посадить 350 саженцев кустов. В первый день они посадили одну седьмую часть всех саженцев. Это в 2 раза меньше, чем во второй день. Поставь вопрос и реши задачу.
Сколько саженцев осталось посадить рабочим?
1) 350 7 = 50 (с.) − посадили рабочие в первый день
2) 50 • 2 = 100 (с.) − посадили рабочие во второй день
3) 350 − (50 + 100) = 350 − 150 = 200 (с.) − осталось посадить
О т в е т: рабочим осталось посадить 200 саженцев.
431. Для математического кружка купили сначала 10 одинаковых калькуляторов, заплатив за них k р., потом купили еще 8 таких же калькуляторов. Запиши выражение, которое обозначает стоимость второй покупки, стоимость первой и второй покупок.
k 10 − цена одного калькулятора
8 • (k 10) − стоимость второй покупкиk + 8 • (k 10) − стоимость первой и второй покупок
432. Составь уравнения и реши их.1) Произведение задуманного числа и числа 8 равно разности чисел 11288 и 2920.2) Частное чисел 2082 и 6 равно сумме задуманного числа и числа 48.
Если x − задуманное число, то:
8 • x = 11288 − 2920
8 • x = 8368x = 8368 8x = 1046
Если x − задуманное число, то:
2082 6 = x + 48x + 48 = 2082 6x + 48 = 347x = 347 − 48x = 299
433. Найди значения выражения α • b при α = 17296 и b = 8, α = 137009 и b = 7.
× 17296 8 138368
× 137009 7 959063
434. Найди значения выражения b : c при b = 7569 и c = 3, b = 345365 и c = 5.
— 7569|3 6 |2523 —15 15 _6 6 _9 9
— 345365|5 30 |69073 —45 45 _36 35 _15 15
435. 658 : 7 9235 + 4 • (536 : ![]() 40077 • 7 − 199099 836 : 4 (2010 − 1065) : 7 • 6 9020 • 6 + 53901
40077 • 7 − 199099 836 : 4 (2010 − 1065) : 7 • 6 9020 • 6 + 53901
— 658|7 63 |94 —28 28 0
— 836|4 8 |209 —36 36 0
9235 + 4 • (536 ![]() = 9235 + 4 • 67 = 9235 + 268 = 9503
= 9235 + 4 • 67 = 9235 + 268 = 9503
— 536|8 48 |67 —56 56 0
× 67 4 268
+ 9235 268 9503
(2010 − 1065) 7 • 6 = 945 7 • 6 = 135 • 6 = 810
_ 2010 1065 945
— 945|7 7 |135 —24 21 _35 35 0
× 135 6 810
40077 • 7 − 199099 = 280539 − 199099 = 81440
×40077 7 280539
_280539 199099 81440
9020 • 6 + 53901 = 54120 + 53901 = 108021
×9020 6 54120
+54120 53901 108021
436. Сравни площади фигур на рисунках. Узнай, на сколько квадратных миллиметров площадь одной фигуры больше площади другой.
Площадь первой фигуры состоит из 2 частей: паруса и судна.
Парус состоит из 23 полных клеток и 4 половинок клеток. Значит, парус состоит из: 23 + 4 2 = 25 полных клеток.
Судно состоит из 9 полных клеток и 4 половинок клеток. Значит, судно состоит из: 9 + 4 2 = 11 полных клеток.
Всего в этой фигуре получается: 25 + 11 = 36 полных клеток.
Так как сторона одной клетки равна 5 мм, то её площадь будет: 5 мм • 5 мм = 25 мм2. Тогда площадь фигуры будет: 25 мм2 • 36 = 900 мм2.
Площадь второй фигуры состоит из 2 частей: паруса и судна.
Парус состоит из 18 полных клеток и 8 половинок клеток. Значит, парус состоит из: 18 + 8 2 = 22 полных клеток.
Судно состоит из 11 полных клеток и 4 половинок клеток. Значит, судно состоит из: 11 + 4 2 = 13 полных клеток.
Всего в этой фигуре получается: 22 + 13 = 35 полных клеток.
Так как сторона одной клетки равна 5 мм, то её площадь будет: 5 мм • 5 мм = 25 мм2. Тогда площадь фигуры будет: 25 мм2 • 35 = 875 мм2.
900 мм2 — 875 мм2 = 25 мм2 — разница площадей первой и второй фигур.
О т в е т: площадь первой фигуры больше площади второй фигуры на 25 мм2.
Проверочные работы, с. 50, 51.
| ← Предыдущая | Следующая → |
Страница 35
Задание 1.
1) Найди среди этих четырёхугольников квадраты и выпиши их номера.
2) Объясни, чем похожи и чем различаются фигуры 1 и 2, 2 и 3, 3 и 4.
- 1) 2, 3.
- 2) 1 — прямоугольник 2 — квадрат, 2 меньше, чем 3, 3 — квадрат 4 не квадрат.
Задание 2.
В одной посылке было 6 кг яблок. Сколько килограммов яблок было в другой посылке, если всего в двух посылках было 14 кг яблок? Составь две задачи, обратные данной. Реши их.
- В одной посылке было 8 кг яблок. Сколько килограммов яблок было в другой посылке, если всего в двух посылках было 14 кг яблок?
- Решение:
- 1) 14 — 8 = 6
- Ответ: 6 кг
- В одной посылке было 6 кг яблок. Сколько килограммов яблок в двух посылках, если в другой было 8 кг яблок?
- Решение:
- 1) 6 + 8 = 14
- Ответ: 14 кг.
Задание 3.
Составь задачу по краткой записи и реши её.
| 1) | 2) |
| Было — 60 м. | Было — ? |
| Уехали — ? | Приехали — 15 м. и 5 м. |
| Осталось — 20 м. | Стало — 60 м. |
Вычисли. Выполни проверку.
| 27 + 73 = 100 | 91 — 45 = 46 | 64 + 28 = 92 | 83 — 69 = 14 |
Реши примеры
| 60 — (43 — 20) = 37 | (28 + 40) — 20 = 48 | 8 — 2 + 7 = 13 |
Составь два выражения со скобками так, чтобы значение каждого было равно 15.
| (4 — 3) + 14 = 15 | 54 — (28 + 11) = 15 |
8 + 7 + 15 + 65 < 7 + 65 + 20 + 8
Площадь прямоугольника
Площади простых фигур, таких как квадратов и прямоугольников рассчитывать научились быстро. Для этого измеряют стороны прямоугольника.
Площадь прямоугольника находится по формуле: S = a ∙ b, где длину надо умножить на ширину фигуры.
Задание 1.
Постройте прямоугольник, длина которого 50 мм, а ширина 30 мм.

Можно ли длину и ширину данного прямоугольника выразить в сантиметрах?
Можно.
|
50 мм = 5 см |
30 мм = 3 см |
Найдите периметр прямоугольника. Р = (a + b) ∙ 2
Р = (5 + 3) ∙ 2 = 16 (см)
Ответ: 16 см
Имеет ли построенная вами фигура площадь?
Да. Прямоугольник имеет длину 5 см и ширину 3 см. Найдем, чему равна площадь прямоугольника по формуле S = a ∙ b.
S = 5 ∙ 3 = 15 см2
Ответ: площадь прямоугольника равна 15 кв.см.
Задание 2.
Чему равна площадь прямоугольника со сторонами 5 см и 4 см? Рассуждаем так. Нам известна длина и ширина прямоугольника. Площадь равна произведению этих величин.
S = 5 ∙ 4 = 20 см2
Ответ: 20 кв.см.
Задание 3.
Рассмотрите следующий рисунок:
Как называется данная геометрическая фигура?
Многоугольник.
Как найти площадь этого многоугольника?
Найти площади отдельных прямоугольников.
Найдите площадь этого многоугольника разными способами.
Первый способ.
Решение.
Измеряем стороны большого прямоугольника.
Длина равна 3 см, а ширина 3 + 1 = 4 (см).
1) 4 · 3 = 12 (см2) – площадь большого прямоугольника.
Длина маленького прямоугольника 3 см, а ширина 1 см. Перемножим эти величины.
2) 3 · 1 = 3 (см2) – площадь маленького прямоугольника.
Теперь из большей фигуры вырезаем два маленьких белых прямоугольника.
3) S = 12 – 3 – 3 = 6 (см2) – площадь многоугольника.
Второй способ.
Решение.
1) 3 · 1 = 3 (см2) – площадь верхнего прямоугольника.
2) 3 · 1 = 3 (см2) – площадь второго прямоугольника.
3) S = 3 + 3 = 6 (см2) – общая площадь многоугольника.
Ответ: S = 6 см2
Страница 40. Что узнали, чему научились.
Задание 1.
Вычисли с устным объяснением и проверкой.
| 1) 32 + 45 = 77 | 68 — 43 = 25 | 54 + 13 = 67 | 79 — 56 = 23 | |
| 2) 57 + 38 = 95 | 73 + 17 = 90 | 64 + 26 = 90 | 87 + 13 = 100 | 42 + 53 = 95 |
| 3) 40 — 18 = 58 | 50 — 24 = 26 | 42 — 18 = 24 | 56 — 27 = 29 | 96 — 43 = 53 |
Задание 3.
Найди значения выражений а + 8 и Ь — 6 при a = 14, a = 8, a = 6, a = 0 и b = 13, b = 18, b = 44, b = 50.
| 14 + 8 = 22 | 8 + 8 = 16 | 6 + 8 = 14 | 0 + 8 = 8 |
| 13 — 6 = 7 | 8 — 6 = 2 | 44 — 6 = 38 | 50 — 6 = 44 |
Выпиши уравнения, решением которых является число 7.
| 15 — x = 8 | x + 40 = 47 | 14 — x = 7 |
| 17 — x = 10 | 16 — x = 9 | 27 — x = 20 |
Задание 5.
Используя числа 21, 14, 8 и 7, составь по 2 верных равенства и неравенства.
21 — 14 = 7
14 + 7 = 21
21 + 7 > 14 + 8
14 + 7 + 8 > 21
Реши примеры
| 80 — (24 — 6) = 62 | 48 + (13 + 7) = 28 | 89 — (64 — 4) = 29 |
| 90 — (36 — |
34 + (18 + 2) = 14 | 75 — (37 — 7) = 45 |
Реши примеры
| 8 + 7 — 6 = 9 | 12 — 7 + 9 = 14 | 6 + 6 — 8 = 4 |
| 4 + 9 — 7 = 6 | 16 — 8 + 7 = 15 | 7 + 7 — 5 = 9 |
Преобразование величин
По формуле S = a ∙ b квадратные сантиметры можно выразить в квадратных метрах. Давайте вспомним, что один метр равен сто сантиметрам.
1 м = 100 см
Мы выполним умножение сторон, и найдем квадратную величину.
Значит: 1 м2 = 100 ∙ 100 = 10000 см2
Задание 4.
Вычислите сколько кв.дм в 1 м2. Во сколько раз 1 кв. м. больше 1 кв. дм?
Как преобразовать квадратные дециметры в квадратные метры? Давайте рассуждать так. Квадрат со стороной 1 м разделим на 10 столбиков. В каждом таком столбике по 10 кв. дм, то есть всего в кв. м 10 десятков, или 100 дм2.
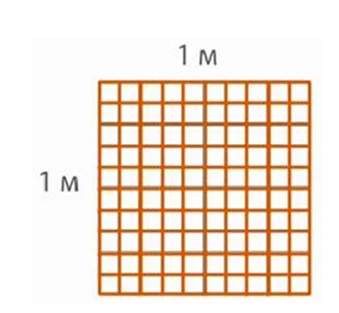
Второй вариант размышлений отталкивается от формулы. Умножаем длину на ширину. 10 дм на 10 дм, получится 100 дм2.
1 м2 = 10 ∙ 10 = 100 дм2
Ответ: в 1 кв. м содержится 100 кв.дм. 1 кв.м. в сто раз больше одного квадратного дециметра.
Задание 5.
Сколько кв. см в 1 кв. дм? Во сколько раз 1 кв. дм. больше 1 кв. см?
Выражаем квадратные дециметры в квадратных сантиметрах.
1 дм = 10 см
1 дм2 = 10 ∙ 10 = 100 см2
Ответ: 1 кв.дм равен 100 кв.см. 1 кв.дм в сто раз больше одного квадратного сантиметра.
Выполните упражнение:
Найдите, сколько квадратных дециметров в 8 м2, в 25 м2, в 45 м2 9 дм2
Мы знаем, что 1 м2 – это 100 дм2, то есть число м2 в 100 раз больше числа дм2, поэтому умножим 8 на 100, получим 800 дм2.
25 м2 : умножим 25 на 100 = 2500 дм2.
45 м2 9 дм2 : это 45 ∙ 100 + 9 = 3100 + 9 = 4509 мм2.
Наш урок подходит к концу.
Продолжите фразу:
сегодня я научился
было интересно
было трудно
Вы хорошо потрудились, поэтому сможете справиться с самостоятельными заданиями.
До новых встреч!
Часть 1:
Числа от 1 до 1000Нумерация
1
2
3
4
5
6
7
8
9
10
?
Четыре арифметических действия: сложение, вычитание, умножение, деление
11
12
13
14
15
16
17
18
19
20
21
22
?
23
24
25
26
27
28
?
29
30
31
32
33
34
35
36
?
37
38
39
40
41
42
43
?
44
45
46
47
48
49
50
51
52
53
?
54
55
56
57
58
59
?
60
61
62
63
64
65
66
67
?
68
69
70
71
72
73
?
74
75
76
77
78
79
80
?
Диаграммы
81
82
83
Страница 18. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Страница 19. Вопросы для повторения
1
2
3
4
Страница 20. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
12
Числа, которые больше 1000Нумерация
84
85
86
87
88
89
90
91
92
93
?
94
95
96
97
98
99
?
100
101
102
103
104
105
106
?
107
108
109
110
111
112
113
114
115
116
?
117
118
119
120
121
122
123
124
?
125
126
127
128
129
130
131
132
133
?
134
135
136
137
138
139
140
141
142
?
143
144
145
146
147
Страница 31. Странички для любознательных
1
2
3
Страница 34. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Страница 35. Вопросы для повторения
1
2
3
4
5
6
7
Величины
148
149
150
151
152
153
154
155
?
156
157
158
159
160
161
162
163
164
165
?
166
167
168
169
170
171
172
173
174
175
176
177
?
178
179
180
181
182
183
184
185
186
187
188
189
190
?
191
192
193
194
195
196
197
198
199
?
200
201
202
203
204
205
206
207
208
?
209
210
211
212
213
214
215
216
?
217
218
219
220
221
222
?
223
224
225
226
227
228
229
230
?
231
232
233
234
235
236
237
238
?
239
240
241
242
243
244
245
?
246
247
248
249
250
251
252
253
?
254
255
256
257
258
259
Страница 53. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Страница 55. Вопросы для повторения
1
2
3
Страница 58. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
10
Вариант 2
1
2
3
4
5
6
7
8
9
10
Сложение и вычитание
260
261
262
263
264
265
266
?
267
268
269
270
271
272
273
274
275
?
276
277
278
279
280
281
282
?
283
284
285
286
287
288
289
290
?
291
292
293
294
295
?
296
297
298
299
300
301
302
303
304
305
?
306
307
308
309
310
311
312
?
313
314
315
316
317
318
?
319
320
321
322
323
324
Страница 69. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
Страница 70. Странички для любознательных
1
2
3
4
Страница 71. Задачи — Расчеты
1
2
Страница 72. Что узнали. Чему научились
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Страница 73. Вопросы для повторения
1
2
3
4
5
6
Страница 74. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
10
Вариант 2
1
2
3
4
5
6
7
8
9
10
Умножение и деление
325
326
327
328
329
330
331
332
?
333
334
335
336
337
338
339
?
340
341
342
343
344
345
346
347
348
349
?
350
351
352
353
354
355
356
?
357
358
359
360
361
362
?
363
364
365
366
367
368
369
370
371
?
372
373
374
375
?
376
377
378
379
?
380
381
382
383
384
385
386
387
?
388
389
390
391
392
393
394
?
395
396
397
398
399
400
401
402
403
?
404
405
406
407
408
409
410
?
411
412
413
414
415
416
417
?
418
419
420
421
422
423
424
425
?
426
427
428
429
430
431
432
433
434
435
436
Страница 91. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Страница 95. Вопросы для повторения
1
2
3
4
5
6
7
8
Страница 96. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
Вариант 2
1
2
3
4
5
6
7
8
9
Тексты для контрольных работСтраница 98. Задания базового уровня
1
2
3
4
5
6
7
8
Страница 99. Задания повышенного уровня сложности
1
2
3
4
5
6
7
8
9
20 Интересных Фактов о «Властелин Колец» — Жизнь Героев за Кадром
- Связь с реальным миром: Ворота Мории, которые появляются в «Братстве Кольца», на самом деле являются входом в национальный парк Фиордланд в Новой Зеландии.
- Изменение кастинга: Изначально роль Арагорна предлагалась Стюарту Таунсенду, но после нескольких недель съемок его сменил Вигго Мортенсен.
- За пределами актерского искусства: Сэмвиз Гэмджи, исполнивший роль Сэма, настоящим именем является Шон Остин, который также снялся в роли режиссера при съемках дополнительных материалов.
- Специальный гость: Писатель Дж.Р.Р. Толкин появляется в фильме «Две Твердыни» в качестве пассажира в поезде в Ривенделл.
- Повседневная жизнь: Чтобы создать атмосферу хоббитской деревни, актеры, игравшие хоббитов, снимались на отдельных наборах, построенных в два раза меньше стандартных.
- Сложные костюмы: Костюмы орков были настолько сложными, что актеры часто не могли сами их надеть, и костюмерам приходилось помогать им.
- Эпический масштаб: Общая продолжительность всех фильмов «Властелин Колец» более 11 часов, делая эту трилогию одной из самых долгих в истории кино.
- Неожиданный фанат: Режиссер Питер Джексон снял камео во всех трех фильмах, играя роль главного плантатора в Новом Зеландии.
- Языковые изыски: Для создания языков Средиземья, Дж.Р.Р. Толкин разработал более 15 искусственных языков, включая кхуздул (язык дварфов) и квеня (язык эльфов).
- Специальный грим: Создание грима для орков и других тварей заняло более 4 часов на каждого актера.
- Настоящая опасность: Шон Бин (Боромир) случайно поранил себя мечом, снимаясь в одной из сцен.
- Сложность сценария: Сценарий к фильмам был написан командой сценаристов, включая самого Питера Джексона, Фрэнсиса Уолш и Филиппу Бойенс, в течение четырех лет.
- Настоящие эффекты: Для создания эффектов взрывов в битве за Хельмову Падь, команда использовала 2500 кг взрывчатки.
- Семейные связи: Сын Шона Бина, актер Элия Бин, также принимал участие в съемках, играя эльфа.
- Специальные места: Для съемок Горы Модор, где расположена Черная Башня, использовали активный вулкан в Новой Зеландии — Маунт Нгаурухое.
- Настоящие эмоции: Исключительная эмоциональная реакция Шона Бина на сцене смерти Боромира была результатом того, что его персонажу действительно нужно было расстаться со своей родной землей.
- Музыкальное волшебство: Музыкальный саундтрек к фильмам был написан Говардом Шором, за что он получил две премии «Оскар».
- Любовь к деталям: Для создания костюмов и реквизита были использованы тысячи физических моделей оружия, доспехов и других предметов.
- Шутки на площадке: Актеры часто играли на камеру футбол и шутили, чтобы сохранять дружественную атмосферу на съемочной площадке.
- Реальные свадьбы: Несколько членов съемочной группы поженились в течение создания трилогии, что придало еще больше семейной атмосферы производству.
Сравнение площадей фигур
Мы можем площади плоских фигур сравнить на глазок. Посмотрите на иллюстрацию.

Картина на стене занимает меньше места, потому говорят, что ее площадь меньше, чем стена. Книги, тетради меньше площади крышки стола. Их как бы наложили сверху, и еще осталось место.
Перечислите способы сравнения фигур по площади.
Можно сравнить на глазок или накладывая предметы, фигуры друг на друга.
Расставьте в порядке уменьшения:
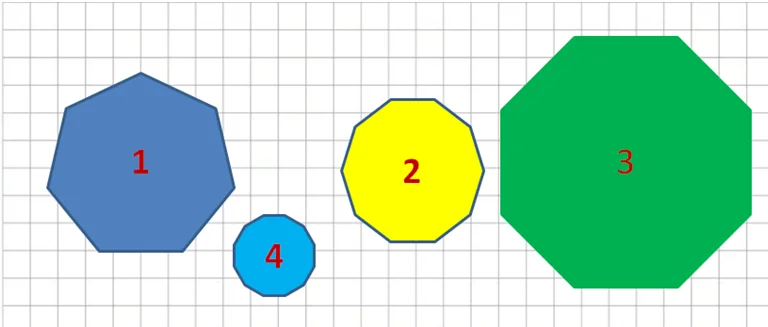
Если получилось так: 3, 1, 2, 4, то вы отлично справились.
Теперь сравните треугольник с кругом:
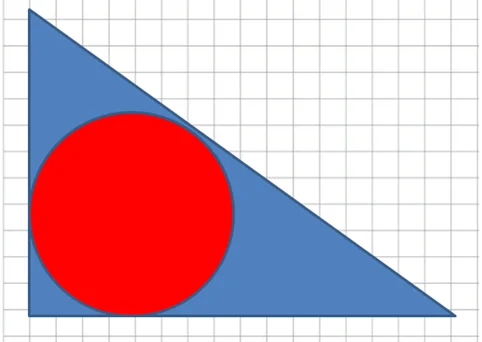
Круг меньше площади треугольника.
Сравнить можно с помощью любых мерок. На рисунке прямоугольники измеряли заданной меркой — треугольником.
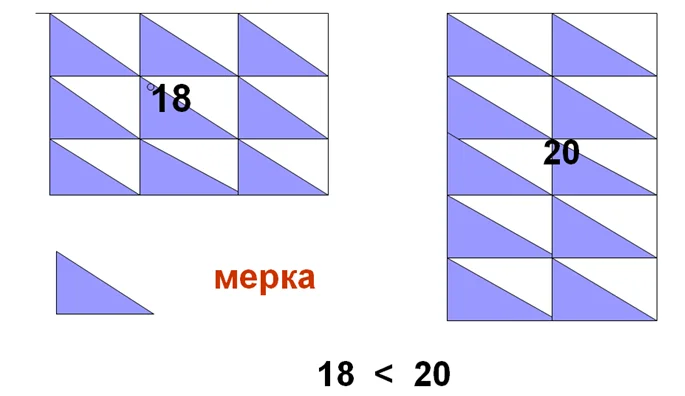
В левый прямоугольник их поместилось 18, а в правый — 20. Делаем вывод, что площадь левой фигуры меньше, чем правой.
Хороший способ сравнения — это подсчет клеток.
Чтобы сравнить площади клетчатых фигур, надо пересчитать количество клеток:
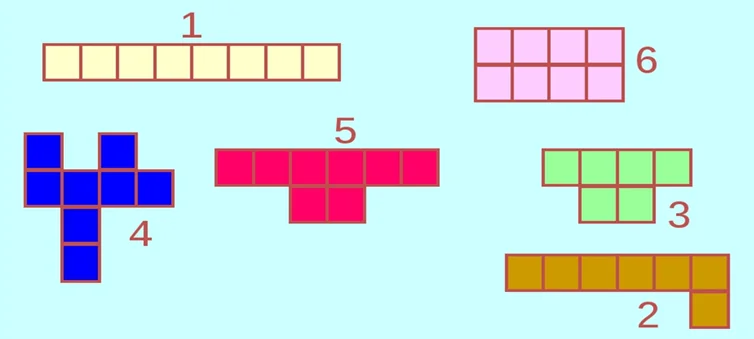
Фигура 3 самая маленькая по площади – 6 клеток. Фигура 2 имеют большую площадь, чем 3. В ней 7 клеток. Площади фигур 1,4,5,6 равновеликие. Они равны 8 клеткам, по площади больше фигур 2 и 3.
Разностное сравнение площадей фигур — это нахождение разницы между большей и меньшей величиной.
Сравните площади фигур 3 и 1. Запишите результаты сравнения.
Проверьте себя:
8 – 6 = 2
Ответ: 2 клетки
Фильмы «Властелин Колец» — Про Что Кинофраншиза?
Фильмы «Властелин Колец» — это кинотрилогия, основанная на романе Дж.Р.Р. Толкина. Сюжет развивается в вымышленном мире Средиземья, где волшебные расы и зловещие силы сталкиваются в борьбе за Властелинство Кольца. Главный герой, Фродо Бэггинс, отправляется в опасное путешествие, чтобы уничтожить Кольцо Всевластия, которое может принести разрушение миру.
Три части фильма — «Братство Кольца», «Две Твердыни» и «Возвращение Короля» — следят за Фродо и его союзниками, включая хоббита Сэма, человека Арагорна, эльфийского лучника Леголаса, гнома Гимли и других, в их эпическом путешествии. Они сталкиваются с врагами, такими как Саурон и Саруман, а также со множеством существ и загадочных ландшафтов.
Фильмы славятся великолепной режиссурой Питера Джексона, визуальными эффектами и захватывающей музыкальной атмосферой
Основанная на литературном наследии, эта кинотрилогия обогатила жанр фэнтези, создав эпическое произведение, которое привлекает внимание зрителей своим богатством мира, персонажей и волнующим сюжетом






























