Можно ли повысить успеваемость с ГДЗ от Моро?
В школе, на уроке, у ребенка в голове формируется общие представления и навыки работы с числами. Именно на уроке ребенок учится таким базовым вещам как вычитание, сложение, умножение, деление. Именно педагог пытается в достаточной мере предоставить и объяснить необходимую информацию, приводя различного рода примеры ко всевозможным исключениям и правилам. Несомненно, что подавляющую часть получаемых знаний ребенок получает в рамках школы, однако не менее важна и самостоятельная работа дома, во внеурочное время.
Речь идет и о своевременном и правильном выполнении домашних заданий, и о повторении пройденных на уроке тем, и об отработке наиболее сложных или непонятных упражнений. Но ребенок не всегда может справиться самостоятельно с такой нагрузкой, а родители не всегда могут ему помочь. Именно в таких ситуациях на помощь приходит сборник готовых задач от Бантовой и Моро. Он способен решить многие проблемы в плане успеваемости ребенка, повысить его уровень знаний и при этом в значительной степени уменьшить затраты во времени.
И так, какие же достоинства есть у этого сборника:
- Задания, предоставленные на сайте, имеют свой определённый номер, что в разы упрощает поиск нужных упражнений;
- Необычайно быстрый доступ к заданиям с любых устройств. Необходимо только наличие интернета на устройстве;
- Наличие нескольких вариантов решения, что позволяет ученику самому выбрать наиболее удобный для него вариант;
- Максимально подробное разъяснение примеров, полезные советы;
Работа сайта происходит в круглосуточном формате, поэтому найти необходимую задачу или пример можно в любое время.
Однако важно отметить, что, не смотря на легкодоступность готовых заданий, цель сборника – не просто предоставить ребенку возможность бездумного списывания готовых решений, без понимания материала. Такой вариант наиболее простой, однако он никак не сможет помочь решить проблемы с успеваемостью
Гораздо лучше и правильнее использовать другой вариант: в начале самостоятельно разобраться с заданием, а затем сверить его с тем решением, которое представлено в решебнике.
Часть 2:
Страница 4
1
2
3
4
5
6
7
8
Страница 5
1
2
3
4
5
6
7
8
9
Страница 7
1
2
3
4
5
6
7
8
9
10
Страница 9
1
2
3
4
5
6
7
8
9
10
Страница 11
1
2
3
4
5
6
7
8
9
10
Страница 13
1
2
3
4
5
6
7
8
9
10
Страница 14
1
2
3
4
5
6
7
8
9
Страница 15
1
2
3
4
5
6
7
8
9
Страница 18
1
2
3
4
5
6
7
8
9
10
Страница 20
1
2
3
4
5
6
7
8
9
Страница 22
1
2
3
4
5
6
7
8
9
10
11
Страница 24
1
2
3
4
5
6
7
8
9
10
Страница 26
1
2
3
4
5
6
7
8
9
10
Страница 28
1
2
3
4
5
6
7
8
9
Страница 30
1
2
3
4
5
6
7
8
9
10
11
Страница 32
1
2
3
4
5
6
7
8
Страница 34
1
2
3
4
5
6
7
8
9
10
Страница 36
1
2
3
4
5
6
7
8
9
10
Страница 37
1
2
3
4
5
6
7
8
9
10
Страница 40
1
2
3
4
5
6
7
8
Страница 42
1
2
3
4
5
6
7
8
9
10
Страница 44
1
2
3
4
5
6
7
8
9
Страница 46
1
2
3
4
5
6
7
8
9
10
Страница 47
1
2
3
4
5
6
7
8
9
10
Страница 50
1
2
3
4
5
6
7
8
9
10
11
Страница 52
1
2
3
4
5
6
7
8
9
Страница 54
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Страница 59
1
2
3
4
5
6
7
8
9
10
11
Страница 60
1
2
3
4
5
6
7
8
9
10
11
12
Страница 63
1
2
3
4
5
6
7
8
9
10
11
Страница 65
1
2
3
4
5
6
7
8
9
10
Страница 68
1
2
3
4
5
6
7
8
9
10
Страница 69
1
2
3
4
5
6
7
8
9
10
11
Страница 71
1
2
3
4
5
6
7
8
9
10
Страница 73
1
2
3
4
5
6
7
8
9
10
Страница 76
1
2
3
4
5
6
7
8
9
10
Страница 77
1
2
3
4
5
6
7
8
9
Страница 79
1
2
3
4
5
6
7
8
9
Страница 80
1
2
3
4
5
6
7
8
9
Страница 82
1
2
3
4
5
6
7
8
9
10
Страница 83
1
2
3
4
5
6
7
8
Страница 85
1
2
3
4
5
6
7
8
9
10
11
Страница 88
1
2
3
4
5
6
7
8
9
Страница 89
1
2
3
4
5
6
7
8
9
10
Страница 91
1
2
3
4
5
6
7
8
9
10
Страница 92
1
2
3
4
5
6
7
8
9
Страница 93
1
2
3
4
5
6
7
8
9
10
Страница 96
1
2
3
4
5
6
7
8
9
10
Страница 97
1
2
3
4
5
6
7
8
9
10
Страница 98
1
2
3
4
5
6
7
8
9
Страница 100
1
2
3
4
5
6
7
8
9
Страница 102
1
2
3
4
5
6
7
8
9
Страница 103
1
2
3
4
5
6
7
8
9
Страница 105
1
2
3
4
5
6
7
8
9
Страница 106
1
2
3
4
5
6
7
8
9
Страница 108
1
2
3
4
5
6
7
8
9
Страница 110
1
2
3
4
5
6
7
8
9
Страница 111
1
2
3
4
5
6
7
8
9
Страница 112
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Страница 116
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Страница 117
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Страница 121
1
2
3
4
5
6
7
Страница 122
1
2
3
4
5
6
Страница 123
1
2
3
4
5
6
7
8
9
10
11
Страница 125
1
2
3
4
5
6
7
8
9
10
11
12
Страница 126
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Самостоятельная работа к урокам 4-9
Построй схему и запиши решение:
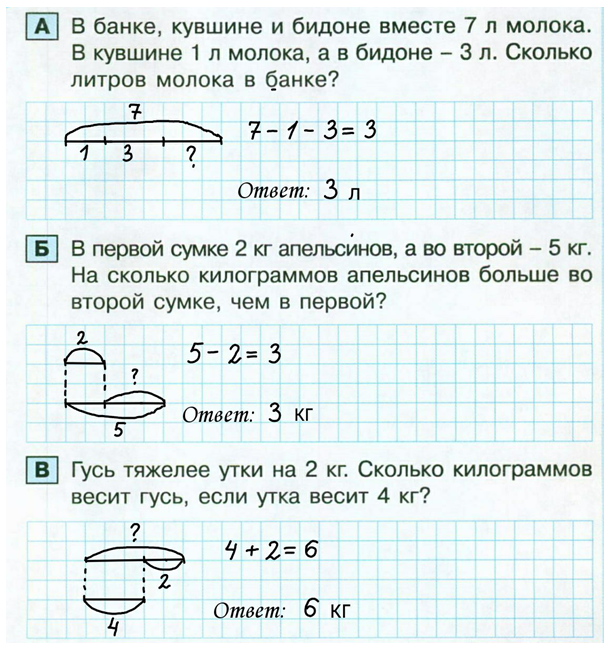
А. В банке, кувшине и бидоне вместе 7 л молока. В кувшине 1 л молока, а в бидоне – 3 л. Сколько литров молока в банке?
Б. В первой сумке 2 кг апельсинов, а во второй – 5 кг. На сколько килограммов апельсинов больше во второй сумке, чем в первой?
В. Гусь тяжелее утки на 2 кг. Сколько килограммов весит гусь, если утка весит 4 кг?
Пояснение:
А. Для удобства нарисуем отрезок, обозначающий общее количество молоко. Мы должны разделить этот отрезок на 3 части: одна маленькая – 1л в кувшине, вторая часть побольше – 3 л в бидоне и третья часть примерное как вторая – молоко в банке. Чтобы найти, сколько молока в банке, надо вычесть известные нам части из целого7-1-3=4 или 7-1=6 и 6-3=3 л.
Б. Нарисуем для удобства отрезок, он будет обозначать апельсины в первой сумке, то есть 2 кг. Снизу нарисуем второй отрезок побольше, начиная отрезок с той же клетки, с которой начали первый отрезок. Второй отрезок обозначает апельсины во второй сумке, то есть 5 кг. Проведем пунктирную линию от конца и начала первого отрезка ко второму отрезку. Так, мы разделим второй отрезок на 2 части, первая из которых будет равна 2 кг, а вторая – разнице между количеством апельсинов в сумках, ее нам и нужно найти. Таким образом, весь второй отрезок – это целое – 5 кг, и он разделён на 2 части: первая – 2 кг, а вторая неизвестна. Чтобы ее найти, нужно из целого – 5 кг, вычесть известную часть – 2 кг: 5-2=3 кг.
В. Для удобства нарисуем 2 отрезка: первый отрезок будет равен весу гуся, а второй – весу утки. Проведем пунктирную линию от конца и начала второго отрезка к первому отрезку. Так, мы разделим первый отрезок на 2 части: первая будет равна 4 кг (вес утки), а вторая – разнице между весом утки и весом гуся – 2 кг. Так, первый отрезок у нас целое – вес гуся, и чтобы его найти, нужно сложить все части вместе: 4+2=6 кг весит гусь.
Ответ:
У брата и сестры конфет было поровну. Потом брат дал сестре 3 конфеты. На сколько конфет стало больше у сестры?
Пояснение:
выражение «поровну» означает, что количество конфет у брата и у сестры изначально было одинаковым. Затем брат отдал сестре 3 конфеты. Это значит, что у брата стало на 3 конфеты меньше, а у сестры на 3 конфеты больше. Допустим, у брата и сестры было по х конфет, тогда сейчас у брата: х-3, а у сестры: х+3. Чтобы найти, на сколько конфет стало больше у сестры, нужно количество конфет у брата вычесть из количества конфет у сестры: х+3-(х-3)=х+3-х+3=6 (обязательно берем выражение х-3 в скобки, чтобы не запутаться со знаками; при их раскрытии + на + дает +, — на – дает -, + на – дает -; если перед х нет -, значит х положительный, то есть перед ним +).
Ответ:
на 6 конфет больше у сестры.
Основные темы, которые представлены в ГДЗ по математике за 4 класс от Моро
В процессе обучения у ребенка могут возникнуть такие моменты, когда возможности попросить помощи просто нет. Конечно, родители всегда желают ребенку только добра и хотят ему помочь: кто-то сидит с ребёнком сам, а кто-то нанимает репетиторов или частных педагогов. Но не все могут позволить оплатить репетитора, или из-за загруженности на работе самостоятельно заниматься уроками с ребенком. Тут то на помощь и может прийти онлайн решебник в 2-х частях по математике за 4 класс, который включает в себя такие темы как:
- Натуральные числа от единицы до тысячи;
- Числа больше тысячи;
- Материал для справок;
- Итоговое повторение пройденного материала;
- Материал, который поможет расширить, углубить и закрепить имеющиеся знания;
Ответы к странице 55
Другие решебники 4 класс:
- Математика
- Русский язык
- Английский язык
- Окружающий мир
- Литературное чтение
Что узнали. Чему научились.
12. Сравни скорости, с которыми могут двигаться разные животные (с. 78—79).
1. 600 м/мин = 600 * 60 = 36000 м/ч = 36 км/ч − скорость аиста.
2. 90 км/ч − скорость голубя.
3. 60 км/ч − скорость воробья.
4. 72 км/ч − скорость колибри.
5. 30 м/с = 30 * 3 600 = 108 000 м/ч = 108 км/ч − скорость гепарда.
6. 25 м/с = 25 * 3 600 = 90 000 м/ч = 90 км/ч − скорость антилопы.
7. 80 км/ч − скорость льва.
8. 500 м/мин = 500 * 60 = 30 000 м/ч = 30 км/ч − скорость страуса.
9. 1 км/мин = 1 * 60 = 60 км/ч − скорость зебры.
10. 750 м/мин = 750 * 60 = 45 000 м/ч = 45 км/ч − скорость жирафа.
13.
1) Дана сумма 36 + 44. Каждое слагаемое увеличили в 20 раз. Проверь, увеличится ли в 20 раз значение суммы.
36 + 44 = 80
36 * 20 + 44 * 20 = 720 + 880 = 1 600
1 600 : 80 = 20 — да, увеличится
2) Дано произведение 15 * 10. Первый множитель увеличили в 4 раза, а второй оставили без изменения. Проверь, увеличится ли в 4 раза значение произведения.
15 * 10 = 150
15 * 4 = 60, 60 * 10 = 600
600 : 150 = 4 — да, увеличится
14.
34 * (120 — 3 920 : 70) = 34 * (120 — 56) = 34 * 64 = 2 176
(110 — 3 420 : 90) * 25 = (110 — 38) * 25 = 72 * 25 = 1 800
15. Выполни деление с остатком.
448 : 10 = 44 (ост. ![]()
683 : 10 = 68 (ост. 3)
367 : 80 = 4 (ост. 47)
421 : 50 = 8 (ост. 21)
293 : 70 = 4 (ост. 13)
16. Составь и реши задачи по рисункам животных (с. 79).Задача 1:
Известно, что гепард может бегать со скоростью 30 м/с, а лев — со скоростью 80 км/ч. Кто из них бегает быстрее и на сколько?
1) 30 м/с = 30 * 3 600 = 108 000 м/ч = 108 (км/ч) — скорость гепарда
2) 108 — 80 = 28 (км/ч) — гепард быстрее льва.Ответ: гепард быстрее льва на 28 км/ч.
Задача 2:
Какое расстояние пробежит зебра за полчаса, если известно, что ее скорость 1 км/мин?
1 ч = 60 мин
полчаса = 60 : 2 = 30 мин.
30 * 1 = 30 (км) — пробежит зебра за полчаса.Ответ: 30 км.
17. Реши задачи и сравни их решения.
1) в один магазин привезли 18 одинаковых бидонов молока, а в другой — 12 таких же бидонов. В первый магазин привезли на 228 л молока больше, чем во второй. Сколько литров молока привезли в каждый магазин?
1) 18 — 12 = 6 (бид.) — на столько больше бидонов привезли в первый магазин.
2) 228 : 6 = 38 (л) — ёмкость одного бидона.
3) 18 * 38 = 684 (л) — молока привезли в первый магазин.
4) 12 * 38 = 456 (л) — молока привезли во второй магазин.Ответ: 684 л и 456 л.
2) в один магазин привезли в одинаковых бидонах 684 л молока, а в другой — 456 л молока в таких же бидонах. В первый магазин привезли на 6 бидонов молока больше, чем во второй. Сколько бидонов молока привезли в каждый магазин?
1) 684 — 456 = 228 (л) — на столько литров больше привезли в первый магазин.
2) 228 : 6 = 38 (л) — ёмкость одного бидона.
3) 684 : 38 = 18 (бид.) — молока привезли в первый магазин.
4) 456 : 38 = 12 (бид.) — молока привезли во второй магазин.
Ответ: 18 бидонов и 12 бидонов.
18. Реши уравнения.
| x — 12 = 0 x = 0 + 12x = 12 |
x : 108 = 1 x = 1 * 108x = 108 |
x * 15 = 0 x = 0 : 15x = 0 |
| 25 + x = 25 x = 25 — 25x = 0 |
y : 1 = 37 y = 37 : 1y = 37 |
x * 18 = 18 x = 18 : 18x = 1 |
19. Начерти и вырежи 4 квадрата со стороной 4 см. Составь из них 2 разных прямоугольника и найди периметр и площадь каждого из них.
1 рисунок:
Площадь: 4 * 16 = 64 см2
Периметр: (4 + 16) * 2 = 20 * 2 = 40 см
2 рисунок:
Площадь: 8 * 8 = 64 см2
Периметр: 8 * 4 = 32 см
20. Рассмотри чертёж и выпиши названия всех треугольников с общей стороной АС; ВС.
Сторона АС: АСD, АСМ, АСB.Сторона BC: BCM, BCA, BCD, BCK, BCO.
21.
1) Объясни, почему на 2 делится без остатка любое число, в записи которого последняя цифра 0, 2, 4, 6 или 8.
Любое число, которое оканчивается на 0, 2, 4, 6 или 8 является четным. Если поделить четное число на 2, то оно всегда делится нацело (без остатка).
2) Какой должна быть последняя цифра в записи числа, которое делится без остатка на 5?
Чтобы число делилось на 5 без остатка, последняя цифра этого числа должна быть 0 или 5.
Задание на полях.
Найди лишнее выражение.
120 * 1 — лишнее, т.к. здесь используется операция умножения, а в других примерах — деление.
- ← предыдущее
- следующее →
Ответы к стр. 40
170. Вырази:
1) в квадратных метрах:
5 км2 = 5 000 000 м2, 500 дм2 = 5 м2;
2) в квадратных миллиметрах:
8 см2 = 800 мм2, 3 см2 20 мм2 = 320 мм2;
3) в квадратных сантиметрах:
2 дм2 = 200 см2, 3 м2 = 30 000 см2;
4) в квадратных дециметрах:
7 м2 = 700 дм2, 900 см2 = 9 дм2.
171. 1) Расстояние между двумя городами 420 км. Поезду на пути из одного города в другой осталось пройти 180 км. На сколько километров больше поезд прошёл, чем ему осталось пройти?
1) 420 – 180 = 240 (км) – прошёл
2) 240 – 180 = 60 (км)
О т в е т: на 60 км прошёл больше, чем осталось.
2) Когда от мотка тесьмы отрезали 3 раза по 2 м, в нём осталось d м. Запиши выражение, которое обозначает, сколько метров тесьмы было в мотке сначала.
2 • 3 + d
172.
954 3 + 512 4 = 446 8 • 8 16 = 4
234 • 4 — 447 • 5 = 201 9 • 8 12 = 6
672 8 — 441 9 = 35 7 • 8 14 = 4
45 000 100 = 450
6 000 • 100 = 600 000
6 000 + 100 = 6 100
173. Выполни деление с остатком и проверь решение.
— 80 |9 Проверка: — 70 |60 Проверка: 72 |8 1) 8 < 9 60 |1 1) 7 < 98 2) 9 • 8 = 72 102) 60 • 1 = 60 3) 72 + 8 = 80 3) 60 + 10 = 70
— 953 |8 Проверка: — 879 |6 Проверка: 8 |119 1) 1 < 8 6 |146 1) 3 < 6 —15 2) х 119 —27 2) х 146 8 8 24 6 —73 952 —39 876 72 3) 952 + 1 = 953 36 3) 876 + 3 = 879 1 3
— 809 |7 Проверка: — 968 |9 Проверка: 7 |115 1) 4 < 7 9 |107 1) 5 < 9 —10 2) х 115 —68 2) х 107 7 7 63 9—39 805 5 963 35 3) 805 + 4 = 809 3) 963 + 5 = 968 4
174. Найди число, которое:
1) больше, чем 567, на 94;
567 + 94 = 661
2) меньше, чем 356, в 4 раза;
356 4 = 89
3) больше, чем разность чисел 946 и 146, в 8 раз.
(946 — 146) • 8 = 6 400
162. Из двух городов, расстояние между которыми 650 км, вышли навстречу друг другу два поезда. Один прошёл 250 км, а другой — на 35 км меньше. На каком расстоянии друг от друга находятся поезда?
1) 250 — 35 = 215 (км) — прошёл 2-й поезд
2) 250 + 215 = 465 (км) — прошли 2 поезда вместе
3) 650 — 465 = 185 (км)О т в е т: расстояние между поездами 185 км.
175. Найди на чертеже прямые, острые и тупые углы. Запиши название каждого угла. Назови виды всех треугольников.
∠ ABC — прямой, ∠ BAK — прямой, ∠ BDK — прямой;
∠ ABD — острый, ∠ BAD — острый, ∠ ADK — острый, ∠ DAK — острый, ∠ CBD — острый, ∠ BDC — острый;
∠ BCD — тупой, ∠ CDK — тупой, ∠ AKD — тупой.
Δ ABD — остроугольный, Δ BCD — тупоугольный, Δ AKD — тупоугольный.
176. Используя знаки действий и скобки, запиши:
1) число 24 четырьмя тройками или тремя двойками (например, 24 = 33 — 3 • 3)
24 = 3 • 3 • 3 — 3
24 = 22 + 2
2) числа 20, 10, 810, 1 008 четырьмя девятками;
20 = 99 9 + 9
10 = (9 • 9 + 9) 9
810 = (99 — 9) • 9
1 008 = 999 + 9
3) число 1 000 пятью девятками или шестью пятёрками.
1 000 = 999 + 9 9
1 000 = (5 + 5) • (5 + 5) • (5 + 5)
177. 1) Как переложить 2 палочки, чтобы получилось 5 одинаковых квадратов?
2) В полученной фигуре убери 2 палочки так, чтобы осталось 3 квадрата.
Во втором задании получается 2 маленьких квадрата и 1 большой.
7 км2 = 7 000 000 м2 800 дм2 = 8 м2
| ← Предыдущая | Следующая → |






























