геометрия — Разделение тупоугольного треугольника на остроугольные
Начнем с комментария Хаген написал:
Итак, можем ли мы решить каждый прямоугольный треугольник таким образом? Чтобы ответить на этот вопрос, я обозначу все свои углы:
Теперь можно составить линейную программу для этих углов от $\alpha_1$ до $\alpha_{21}$ и одного дополнительного угла $\varepsilon$. Правила линейной программы таковы:
- Сумма углов для каждого из семи маленьких треугольников должна быть $180°$.
- В каждой вершине, инцидентной более чем одному треугольнику, сумма углов падения должна составлять $180°$, за исключением $\alpha_6+\alpha_7=90°$ и $\alpha_{17}+\alpha_{18}+\alpha_{19}+\alpha_{20}+\alpha_{21}=360°$.
- Все углы должны быть строго больше $0°$, что я выражаю как $\alpha_i\ge\varepsilon$.
- Все углы должны быть строго меньше $90°$, что я выражаю как $\alpha_i\le90°-\varepsilon$.
- $\varepsilon$ должно быть строго больше нуля, что мы и должны обеспечить, включив его в нашу целевую функцию.
Теперь можно искать решения этой линейной программы. Я так и сделал, пытаясь минимизировать $10\alpha_1-\varepsilon$. Или, выражаясь иначе, я пытался сделать прямоугольный треугольник далеко от равнобедренного, но в то же время старался избегать как нулевых, так и прямых углов. 9{-10} &
\alpha_{8}&=75,0558118504°&
\alpha_{15}&=54,2736044438° \\
\alpha_{2}&=89,9999999997°&
\alpha_{9}&=60,1977531668° &
\alpha_{16}&=89,9999999999° \\
\alpha_{3}&=89,9999999998°&
\alpha_{10}&=44,7464349828°&
\alpha_{17}&=70,0447167828° \\
\alpha_{4}&=44,3278546796°&
\alpha_{11}&=45,2535650175°&
\alpha_{18}&=81,3985408766° \\
\alpha_{5}&=45,6721453206°&
\alpha_{12}&=60,5175473216°&
\alpha_{19}&=79.9759354909° \\
\alpha_{6}&=54,3519191885° &
\alpha_{13}&=74,2288876609°&
\alpha_{20}&=69,2961073381° \\
\alpha_{7}&=35,6480808115° &
\alpha_{14}&=35,7263955563°&
\alpha_{21}&=59,2846995116°
\end{align*}
Итак, как видите, решение было очень вырожденным, с $\alpha_1$ действительно близким к нулю.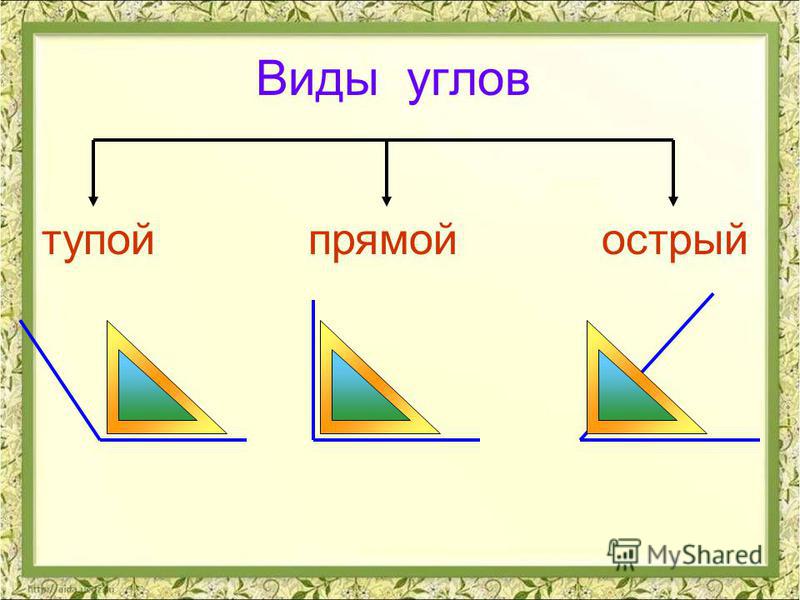
Если подумать, небольшие отклонения от $0°$ соотв. $90°$ в приведенных выше числах, вероятно, являются артефактом работы решателя. Другой решатель дал мне результаты, в которых углы были точно равны $0°$ соответственно. $90°$. И имеет смысл предположить, что вы можете достичь $0°$, если допустите $90°$, и что это лучше с точки зрения целевой функции, чем выше. Чтобы фактически запретить эти решения для всех решателей, вероятно, потребуется фиксированная ненулевая нижняя граница $\varepsilon$.
4 класс. Моро. Учебник №1. Ответы к стр. 40
Величины.
Ответы к стр. 40
170. Вырази:
1) в квадратных метрах:
5 км2 = 5 000 000 м2, 500 дм2 = 5 м2;
2) в квадратных миллиметрах:
8 см2 = 800 мм2, 3 см2 20 мм2 = 320 мм2;
3) в квадратных сантиметрах:
2 дм2 = 200 см2, 3 м2 = 30 000 см2;
4) в квадратных дециметрах:
7 м2 = 700 дм2, 900 см2 = 9 дм2.
171. 1) Расстояние между двумя городами 420 км. Поезду на пути из одного города в другой осталось пройти 180 км. На сколько километров больше поезд прошёл, чем ему осталось пройти?
1) 420 – 180 = 240 (км) – прошёл2) 240 – 180 = 60 (км)О т в е т: на 60 км прошёл больше, чем осталось.
2) Когда от мотка тесьмы отрезали 3 раза по 2 м, в нём осталось d м. Запиши выражение, которое обозначает, сколько метров тесьмы было в мотке сначала.
2 • 3 + d
172.
954 3 + 512 4 = 446 8 • 8 16 = 4234 • 4 — 447 • 5 = 201 9 • 8 12 = 6672 8 — 441 9 = 35 7 • 8 14 = 4
45 000 100 = 4506 000 • 100 = 600 0006 000 + 100 = 6 100
173. Выполни деление с остатком и проверь решение.
— 80 |9 Проверка: — 70 |60 Проверка: 72 |8 1) 8 < 9 60 |1 1) 7 < 98 2) 9 • 8 = 72 102) 60 • 1 = 60 3) 72 + 8 = 80 3) 60 + 10 = 70
— 953 |8 Проверка: — 879 |6 Проверка: 8 |119 1) 1 < 8 6 |146 1) 3 < 6 —15 2) х 119 —27 2) х 146 8 8 24 6 —73 952 —39 876 72 3) 952 + 1 = 953 36 3) 876 + 3 = 879 1 3
— 809 |7 Проверка: — 968 |9 Проверка: 7 |115 1) 4 < 7 9 |107 1) 5 < 9 —10 2) х 115 —68 2) х 107 7 7 63 9 —39 805 5 963 35 3) 805 + 4 = 809 3) 963 + 5 = 968 4
174. Найди число, которое:
1) больше, чем 567, на 94;
567 + 94 = 661
2) меньше, чем 356, в 4 раза;
356 4 = 89
3) больше, чем разность чисел 946 и 146, в 8 раз.
(946 — 146) • 8 = 6 400
162. Из двух городов, расстояние между которыми 650 км, вышли навстречу друг другу два поезда. Один прошёл 250 км, а другой — на 35 км меньше. На каком расстоянии друг от друга находятся поезда?
1) 250 — 35 = 215 (км) — прошёл 2-й поезд2) 250 + 215 = 465 (км) — прошли 2 поезда вместе3) 650 — 465 = 185 (км)О т в е т: расстояние между поездами 185 км.
175. Найди на чертеже прямые, острые и тупые углы. Запиши название каждого угла. Назови виды всех треугольников.
∠ ABC — прямой, ∠ BAK — прямой, ∠ BDK — прямой;∠ ABD — острый, ∠ BAD — острый, ∠ ADK — острый, ∠ DAK — острый, ∠ CBD — острый, ∠ BDC — острый;∠ BCD — тупой, ∠ CDK — тупой, ∠ AKD — тупой.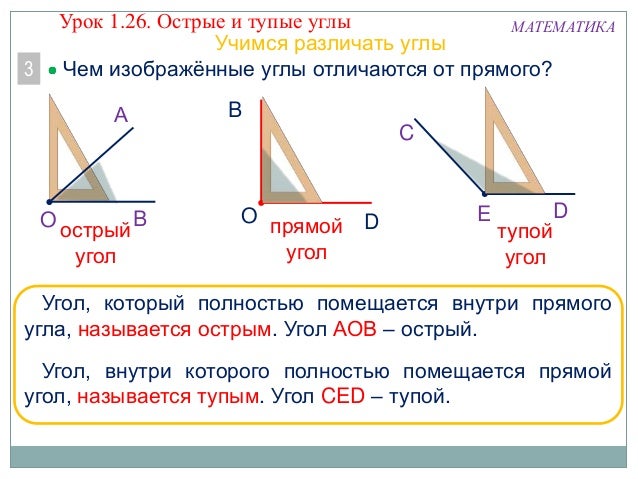
Δ ABD — остроугольный, Δ BCD — тупоугольный, Δ AKD — тупоугольный.
176. Используя знаки действий и скобки, запиши:1) число 24 четырьмя тройками или тремя двойками (например, 24 = 33 — 3 • 3)
24 = 3 • 3 • 3 — 324 = 22 + 2
2) числа 20, 10, 810, 1 008 четырьмя девятками;
20 = 99 9 + 910 = (9 • 9 + 9) 9810 = (99 — 9) • 91 008 = 999 + 9
3) число 1 000 пятью девятками или шестью пятёрками.
1 000 = 999 + 9 91 000 = (5 + 5) • (5 + 5) • (5 + 5)
177. 1) Как переложить 2 палочки, чтобы получилось 5 одинаковых квадратов?
2) В полученной фигуре убери 2 палочки так, чтобы осталось 3 квадрата.
Во втором задании получается 2 маленьких квадрата и 1 большой.
7 км2 = 7 000 000 м2 800 дм2 = 8 м2
ГДЗ по математике.
Учебник.Часть 1.
Математика. 4 класс






























