Дополнительные комментарии и объяснения:
«ГДЗшник.ru» не только предлагает готовые ответы, но и дает дополнительные комментарии и объяснения к решениям. Это позволяет лучше понять материал, исправить ошибки и запомнить правильный подход к задачам. Таким образом, сервис становится не только инструментом для проверки, но и обучающим ресурсом.
Итак, если вам нужно быстро и бесплатно найти решения домашних заданий, обратитесь к сервису «ГДЗшник.ру». Удобство использования, бесплатность, актуальность информации и дополнительные комментарии делают этот ресурс отличным помощником для школьников. Не теряйте времени на поиски — «ГДЗшник.ру» поможет вам успешно справиться с учебными заданиями!
На ГДЗшник.ru вы найдете не только готовые ответы, но и подробные разъяснения к ним, что поможет вам глубже понять учебный материал и успешно справиться с домашними заданиями. Не забывайте использовать ГДЗ как инструмент для обучения и развития, а не как способ легкого пути к решению задач.
Движение в противоположных направлениях
Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:
Скорость удаления больше скорости любого из них.
Задача 1
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?
Решение:
Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.
1.
Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.
2.
Ответ: Через три часа расстояние между переходами будет 27 км.
Задача 2
Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?
Решение:
Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:
1.
Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.
2.
Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.
3.
Ответ:Скорость второго пешехода – 4 км/ч.
Задача 3
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?
Решение:
1) 70+45=115 (км/ч) скорость удаления поездов
2) 115∙2=230 (км) пройдут поезда вместе за 2 часа
3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.
Ответ: Через 2 часа расстояние между поездами составит 250 км.
Задача 4
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?
Решение:
1) 60+40=100 (км/ч) скорость удаления мотоциклистов
2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.
Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.
Часть 2:
Страница 4
1
2
3
4
5
6
7
8
Страница 5
1
2
3
4
5
6
7
8
9
Страница 7
1
2
3
4
5
6
7
8
9
10
Страница 9
1
2
3
4
5
6
7
8
9
10
Страница 11
1
2
3
4
5
6
7
8
9
10
Страница 13
1
2
3
4
5
6
7
8
9
10
Страница 14
1
2
3
4
5
6
7
8
9
Страница 15
1
2
3
4
5
6
7
8
9
Страница 18
1
2
3
4
5
6
7
8
9
10
Страница 20
1
2
3
4
5
6
7
8
9
Страница 22
1
2
3
4
5
6
7
8
9
10
11
Страница 24
1
2
3
4
5
6
7
8
9
10
Страница 26
1
2
3
4
5
6
7
8
9
10
Страница 28
1
2
3
4
5
6
7
8
9
Страница 30
1
2
3
4
5
6
7
8
9
10
11
Страница 32
1
2
3
4
5
6
7
8
Страница 34
1
2
3
4
5
6
7
8
9
10
Страница 36
1
2
3
4
5
6
7
8
9
10
Страница 37
1
2
3
4
5
6
7
8
9
10
Страница 40
1
2
3
4
5
6
7
8
Страница 42
1
2
3
4
5
6
7
8
9
10
Страница 44
1
2
3
4
5
6
7
8
9
Страница 46
1
2
3
4
5
6
7
8
9
10
Страница 47
1
2
3
4
5
6
7
8
9
10
Страница 50
1
2
3
4
5
6
7
8
9
10
11
Страница 52
1
2
3
4
5
6
7
8
9
Страница 54
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Страница 59
1
2
3
4
5
6
7
8
9
10
11
Страница 60
1
2
3
4
5
6
7
8
9
10
11
12
Страница 63
1
2
3
4
5
6
7
8
9
10
11
Страница 65
1
2
3
4
5
6
7
8
9
10
Страница 68
1
2
3
4
5
6
7
8
9
10
Страница 69
1
2
3
4
5
6
7
8
9
10
11
Страница 71
1
2
3
4
5
6
7
8
9
10
Страница 73
1
2
3
4
5
6
7
8
9
10
Страница 76
1
2
3
4
5
6
7
8
9
10
Страница 77
1
2
3
4
5
6
7
8
9
Страница 79
1
2
3
4
5
6
7
8
9
Страница 80
1
2
3
4
5
6
7
8
9
Страница 82
1
2
3
4
5
6
7
8
9
10
Страница 83
1
2
3
4
5
6
7
8
Страница 85
1
2
3
4
5
6
7
8
9
10
11
Страница 88
1
2
3
4
5
6
7
8
9
Страница 89
1
2
3
4
5
6
7
8
9
10
Страница 91
1
2
3
4
5
6
7
8
9
10
Страница 92
1
2
3
4
5
6
7
8
9
Страница 93
1
2
3
4
5
6
7
8
9
10
Страница 96
1
2
3
4
5
6
7
8
9
10
Страница 97
1
2
3
4
5
6
7
8
9
10
Страница 98
1
2
3
4
5
6
7
8
9
Страница 100
1
2
3
4
5
6
7
8
9
Страница 102
1
2
3
4
5
6
7
8
9
Страница 103
1
2
3
4
5
6
7
8
9
Страница 105
1
2
3
4
5
6
7
8
9
Страница 106
1
2
3
4
5
6
7
8
9
Страница 108
1
2
3
4
5
6
7
8
9
Страница 110
1
2
3
4
5
6
7
8
9
Страница 111
1
2
3
4
5
6
7
8
9
Страница 112
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Страница 116
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Страница 117
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Страница 121
1
2
3
4
5
6
7
Страница 122
1
2
3
4
5
6
Страница 123
1
2
3
4
5
6
7
8
9
10
11
Страница 125
1
2
3
4
5
6
7
8
9
10
11
12
Страница 126
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч).
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
3) 160 : 20 = 8 (ч).
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
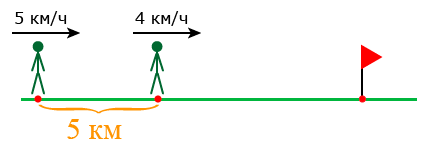
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч).
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
2) 5 : 1 = 5 (ч).
Ответ: Через 5 часов второй пешеход догонит первого.
Часть 2:
стр. 2
стр. 3
стр. 4
стр. 5
стр. 6
стр. 7
стр. 8
стр. 9
стр. 10
стр. 11
стр. 12
стр. 13
стр. 14
стр. 15
стр. 16
стр. 17
стр. 18
стр. 19
стр. 20
стр. 21
стр. 22
стр. 23
стр. 24
стр. 25
стр. 26
стр. 27
стр. 28
стр. 29
стр. 30
стр. 31
стр. 32
стр. 33
стр. 34
стр. 35
стр. 36
стр. 37
стр. 38
стр. 39
стр. 40
стр. 41
стр. 42
стр. 43
стр. 44
стр. 45
стр. 46
стр. 47
стр. 48
стр. 49
стр. 50
стр. 51
стр. 52
стр. 53
стр. 54
стр. 55
стр. 56
стр. 57
стр. 58
стр. 59
стр. 60
стр. 61
стр. 62
стр. 63
стр. 64
стр. 65
стр. 66
стр. 67
стр. 68
стр. 69
стр. 70
стр. 71
стр. 72
стр. 73
стр. 74
стр. 75
стр. 76
стр. 77
стр. 78
стр. 79
стр. 80
стр. 81
стр. 82
стр. 83
стр. 84
стр. 85
стр. 86
стр. 87
стр. 88
стр. 89
стр. 90
стр. 91
стр. 92
стр. 93
стр. 94
стр. 95
стр. 96
стр. 97
стр. 98
стр. 99
стр. 100
стр. 101
стр. 102
стр. 103
стр. 104
стр. 105
стр. 106
стр. 107
стр. 108
стр. 109
стр. 110
стр. 111
стр. 112
стр. 113
стр. 114
стр. 115
стр. 116
стр. 117
стр. 118
стр. 119
стр. 120
стр. 121
стр. 122
стр. 123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
147
148
149
150
151
152
153
154
155
156
157
Числа от 1 до 1000 Умножение на числа, оканчивающиеся нулямиПисьменное умножение двух чисел, оканчивающихся нулямиОтветы к стр. 16
Учимся решать задачи: выполнять схематические чертежи, сравнивать задачи и их решения.
61. Реши задачи, сравни решения.1) Два лыжника вышли одновременно навстречу друг другу из двух поселков и встретились через 3 ч. Первый лыжник шел со скоростью 12 км/ч, а второй − со скоростью 14 км/ч. Найди расстояние между поселками.

2) Из двух поселков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шел со скоростью 12 км/ч, а второй со скоростью 14 км/ч. Через сколько часов лыжники встретились?

3) Из двух поселков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шел со скоростью 12 км/ч. С какой скоростью шел второй лыжник?

1-я задача
1) 12 • 3 = 36 (км) − прошел первый лыжник
2) 14 • 3 = 42 (км) − прошел второй лыжник
3) 36 + 42 = 78 (км)
О т в е т: расстояние между поселками 78 км.
2-я задача
1) 12 + 14 = 26 (км/ч) − скорость сближения лыжников
2) 78 26 = 3 (ч)
О т в е т: время лыжников в пути до встречи 3 часа.
3-я задача
1) 78 3 = 26 (км/ч) − скорость сближения лыжников
2) 26 − 14 = 14 (км/ч)
О т в е т: скорость второго лыжника 14 км/ч.
В первом случае мы искали расстояние между поселками, умножив скорости лыжников на время в пути до встречи и сложив результаты. Во втором — время лыжников до встречи, сложив скорости лыжников и разделив расстояние между поселками на этот результат. А в третьем — скорость второго лыжника, разделив расстояние между городами на время в пути и отняв от этого результат скорость первого лыжника.
62. Составь и реши три похожие задачи про пешеходов, которые шли навстречу друг другу со скоростями 4 км/ч и 5 км/ч и встретились через 2 ч.
1-я задача.
Два пешехода вышли одновременно навстречу друг другу из двух поселков и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч, а второй − со скоростью 5 км/ч. Найди расстояние между поселками.
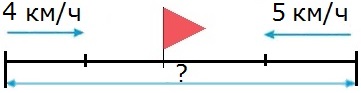
1) 4 • 2 = 8 (км) − прошел первый пешеход
2) 5 • 2 = 10 (км) − прошел второй пешеход
3) 8 + 10 = 18 (км)
О т в е т: расстояние между поселками 18 км.
2-я задача.
Из двух поселков, расстояние между которыми 18 км, вышли одновременно навстречу друг другу два пешехода. Первый из них шел со скоростью 4 км/ч, а второй со скоростью 5 км/ч. Через сколько часов пешеходы встретились?
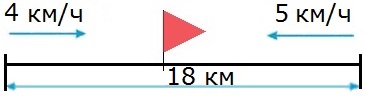
1) 4 + 5 = 9 (км/ч) − скорость сближения пешеходов
2) 18 9 = 2 (ч)
О т в е т: пешеходы встретились через 2 часа.
3-я задача
Из двух поселков, находящихся на расстоянии 18 км, вышли одновременно навстречу друг другу два пешехода и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч. С какой скоростью шел второй пешеход?
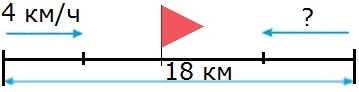
1) 18 2 = 9 (км/ч) − скорость сближения пешеходов
2) 9 − 4 = 5 (км/ч)
О т в е т: скорость второго пешехода 5 км/ч.
63. (Устно.) 600 : 3 + 7 • 5 40 • (16 − ![]() • 2 600 : (3 + 7) • 5 40 • (16 − 8 • 2)
• 2 600 : (3 + 7) • 5 40 • (16 − 8 • 2)
600 3 + 7 • 5 = 200 + 35 = 235
600 (3 + 7) • 5 = 600 10 • 5 = 60 • 5 = 300
40 • (16 − ![]() • 2 = 40 • 8 • 2 = 320 • 2 = 640
• 2 = 40 • 8 • 2 = 320 • 2 = 640
40 • (16 − 8 • 2) = 40 • (16 − 16) = 40 • 0 = 0
64. 8070 • 600 5010 − 15900 : 100 + 786
×8070 600 4842000
5010 − 15900 100 + 786 = 5010 − 159 + 786 = 4851 + 786 = 5637_ 5010 +4851 159 786 4851 5637
9800 • 30 30200 − 7020 : 10 • 3 + 68
×9800 30 294000
30200 − 7020 10 • 3 + 68 = 30200 — 702 • 3 + 68 = 28094 + 68 = 28162×702 +30200 3 2106
2106 28094
ЗАДАНИЕ НА ПОЛЯХЦЕПОЧКА
| ← Предыдущая | Следующая → |





















